题目内容
先阅读下面材料,然后解答问题:王老师在黑板上出了这样一道习题:设方程2x2-5x+k=0的两个实数根是x1,x2,请你选取一个适当的k值,求
| x2 |
| x1 |
| x1 |
| x2 |
小明同学取k=4,则方程是2x2-5x+4=0.
由根与系数的关系,得x1+x2=
| 5 |
| 2 |
∴
| x2 |
| x1 |
| x1 |
| x2 |
| x22+x12 |
| x1x2 |
| (x1+x2)2-2x1x2 |
| x1x2 |
| ||
| 2 |
| 9 |
| 8 |
即
| x2 |
| x1 |
| x1 |
| x2 |
| 9 |
| 8 |
问题(1):请你对小明解答的正误作出判断,并说明理由.
问题(2):请你另取一个适当的正整数k,其它条件不变,不解方程,改求|x1-x2|的值.
分析:(1)使用根与系数的关系列式计算时要先判断该方程是否存在实根,然后再代入数值计算;
(2)要求|x1-x2|的值可以把它变形为|x1-x2|=
,然后利用根与系数的关系即可求出值.
(2)要求|x1-x2|的值可以把它变形为|x1-x2|=
| (x1+x2)2-4x1x2 |
解答:解:(1)小明的解法是错误的.
∵当k=4时,△=25-4×2×4=25-32=-7<0,
∴方程2x2-5x+4=0没有实数根,
本题无解.
所以他选择的k不正确;
(2)(本题答案不唯一,k可以取1、2、3)
如:取k=3时,方程2x2-5x+3=0
∴△=25-4×2×3=25-24=1>0
由根与系数关系得
x1+x2=
,x1x2=
,
∴|x1-x2|=
=
=
.
∵当k=4时,△=25-4×2×4=25-32=-7<0,
∴方程2x2-5x+4=0没有实数根,
本题无解.
所以他选择的k不正确;
(2)(本题答案不唯一,k可以取1、2、3)
如:取k=3时,方程2x2-5x+3=0
∴△=25-4×2×3=25-24=1>0
由根与系数关系得
x1+x2=
| 5 |
| 2 |
| 3 |
| 2 |
∴|x1-x2|=
| (x1+x2)2-4x1x2 |
|
| 1 |
| 2 |
点评:解题时一定要认真审题,周密考虑问题.在利用根与系数的关系解决问题时经常与根的判别式相联系.

练习册系列答案
相关题目

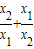 的值.
的值. ,x1x2=2.
,x1x2=2.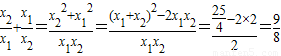
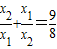 .
.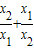 的值.
的值. ,x1x2=2.
,x1x2=2.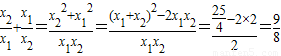
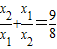 .
.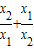 的值.
的值. ,x1x2=2.
,x1x2=2.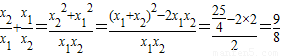
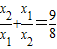 .
.