题目内容
【题目】如图,已知O为直线AD上一点,OB是∠AOC内部一条射线且满足∠AOB与∠AOC互补,OM,ON分别为∠AOC,∠AOB的平分线.
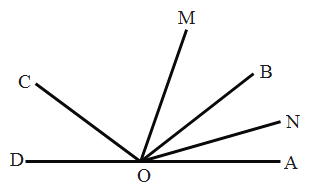
(1)∠COD与∠AOB相等吗?请说明理由;
(2)若∠AOB=30°,试求∠AOM与∠MON的度数;
(3)若∠MON=42°,试求∠AOC的度数.
【答案】(1)相等,理由见解析;(2)∠AOM=75°,∠MON=60°;(3)132°
【解析】
(1)由题意可得∠AOC+∠AOB=180°,∠AOC+∠DOC=180°,可以根据同角的补角相等得到∠COD=∠AOB;
(2)根据互补的定义可求∠AOC,再根据角平分线的定义可求∠AOM,根据角平分线的定义可求∠AON,根据角的和差关系可求∠MON的度数;
(3)设∠AOB=x°,则∠AOC=180°-x°,列方程![]() ,解方程即可求解.
,解方程即可求解.
(1)∵∠AOC与∠AOB互补,
∴∠AOC+∠AOB=180°,
∵∠AOC+∠DOC=180°,
∴∠COD=∠AOB;
(2)∵∠AOB与∠AOC互补,∠AOB=30°,
∴∠AOC=180°-30°=150°,
∵OM为∠AOB的平分线,
∴∠AOM=75°,
∵ON为∠AOB的平分线,
∴∠AON=15°,
∴∠MON=75°-15°=60°;
(3)设∠AOB=x°,则∠AOC=180°-x°.
由题意,得![]()
∴180-x-x=84,
∴-2x=-96,
解得x=48,
故∠AOC=180°-48°=132°.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目