题目内容
在?ABCD中，对角线相交于点O，给出下列条件：①AB=CD，AD=BC，②AD=AB，AD∥BC，③AB∥CD，AD∥BC，④AO=CO，BO=DO其中能够判定ABCD是平行四边形的有
①②③④
①②③④
．分析：根据平行四边形的判定（①有两组对角分别相等的四边形是平行四边形，②有两组对边分别相等的四边形是平行四边形，③有两组对边分别平行的四边形是平行四边形，④有一组对边平行且相等的四边形是平行四边形，⑤对角线互相平分的四边形是平行四边形）推出即可．
解答：解：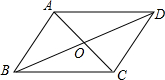
∵AB=CD，AD=BC，
∴四边形ABCD是平行四边形，∴①正确；
∵AD=BC，AD∥BC，
∴四边形ABCD是平行四边形，∴②正确；
∵AB∥CD，AD∥BC，
∴四边形ABCD是平行四边形，∴③正确；
∵AO=CO，BO=DO，
∴四边形ABCD是平行四边形，∴④正确；
即其中能判定四边形ABCD是平行四边形的有①②③④，
故答案为：①②③④．
∵AB=CD，AD=BC，∴四边形ABCD是平行四边形，∴①正确；
∵AD=BC，AD∥BC，
∴四边形ABCD是平行四边形，∴②正确；
∵AB∥CD，AD∥BC，
∴四边形ABCD是平行四边形，∴③正确；
∵AO=CO，BO=DO，
∴四边形ABCD是平行四边形，∴④正确；
即其中能判定四边形ABCD是平行四边形的有①②③④，
故答案为：①②③④．
点评：本题考查了对平行四边形的判定的应用，注意：平行四边形的判定定理有：①有两组对角分别相等的四边形是平行四边形，②有两组对边分别相等的四边形是平行四边形，③有两组对边分别平行的四边形是平行四边形，④有一组对边平行且相等的四边形是平行四边形，⑤对角线互相平分的四边形是平行四边形．
练习册系列答案
相关题目
=∠DCE．
在下面推理过程的括号内填上推理的依据
、∠B＋∠C＝
时，边AB与CD的关系是________．
ABCD中，∠BAC＝
，∠BCA＝
，则∠B＝________．