��Ŀ����
����Ŀ�����Ķ����ϣ��ٽ���������⣺
�����Ѿ�֪��������ʽ�����ʽ��˵ķ��������ƽ�漸��ͼ�ε��������ʾ��ʵ���ϻ���һЩ�������ʽҲ������������ʽ��ʾ�����磺(2a��b) (a��b)��2a2��3ab��b2�Ϳ�����ͼ�ٻ�ͼ�ڵ�ͼ�ε��������ʾ��
(1)��д��ͼ������ʾ�Ĵ������ʽ��
(2)����һ������ͼ�Σ�ʹ��������ܱ�ʾ(a��b��c)2��a2��b2��c2��2ab��2ac��2bc��
(3)�������������д����һ����a��b�Ĵ������ʽ����������֮��Ӧ�ļ���ͼ�Σ�
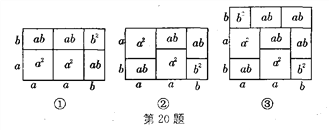
���𰸡�(1)(a��2b)(2a��b)��2a2��5ab��2b2��(2)��������(3)������.
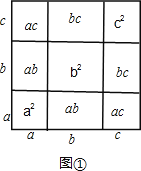
�������������������1�����ݳ�Ϊ2a+b����Ϊa+2b�ľ����������2���߳�Ϊa�������Ρ�1���߳�Ϊb�������Ρ�3����Ϊa��Ϊb�ľ�������ͣ��ɵõ�ʽ����2����һ���߳�Ϊa+b+c�������Σ����ɵã���3����Ψһ���磺��x+p����x+q��=x2+��p+q�� x+pq������Ϊx+q����Ϊx+p�ľ��μ��ɵã�
���������(1)(2a+b)(a+2b)=2 a2+2a��2b+ a��b+ b2=2a2��5ab��2b2��
(2)��ͼ�٣�
(3)(x+p)(x+q)=x2+(p+q)x+pq��
��ͼ�ڣ�
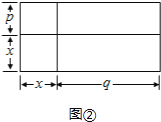
�ʴ�Ϊ��(1)(2a+b)(a+b)=2a2+3ab+b2.

 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�����Ŀ�����人��������̨��֯��һ�κ�����д�����У�10������ѡ�ֵ÷�������£�
���� | 3 | 4 | 2 | 1 |
���� | 80 | 85 | 90 | 95 |
��ô��10��ѡ�����÷�������λ���������ֱ��ǣ� ��
A. 85��85 B. 85.5��85 C. 85��4 D. 85.5��4