��Ŀ����
����Ŀ���۲����а�һ���������е���������
1����2��4����8��16����32��64������������
4�� 1�� 7����5��19����29��67���������� ��
��2��1����5��7����17��31����65�������� ��
��1���ڢ������ĵ�10������________��
��2���ڢ������ĵ�n������________��
��3��ȡÿ�����ĵ�m�������Ƿ����m��ֵ��ʹ���������ĺ͵���1026�������ڣ����m��ֵ���������ڣ���˵������.
���𰸡�(1)-512;(2) ![]() ,(3)11,���ɼ�����
,(3)11,���ɼ�����
�������������������1���۲첻�ѷ��֣��ڢ�������һ������ǰһ�����ģ�-2������д����n��ı���ʽ��Ȼ���n=10������м��㼴�ɵý⣻
��2�������е�ÿ�����ȵ����е�ÿ������3���ó���n�����ʽ;
��3�����ݸ��еĵ�n�����ı���ʽ�г����̣�Ȼ��ⷽ�̼��ɣ�
���������
(1)��Ϊ���������Ĺ���Ϊ![]() ��
��
���Ե��������ĵ�10������-512.
(2)��Ϊ�����е�ÿ�����ȵ����е�ÿ������3�����Ե����еĵ�n����Ϊ![]() .
.
(3)�����е����Ĺ���Ϊ![]() ������ȡÿ�����ĵ�m����������m��ֵ��ʹ���������ĺ͵���1026���ɵ÷���
������ȡÿ�����ĵ�m����������m��ֵ��ʹ���������ĺ͵���1026���ɵ÷���![]() ����
����![]() ,��ã�m=11
,��ã�m=11

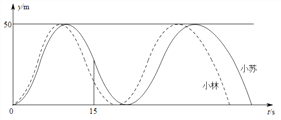
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�