题目内容
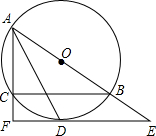 (2013•随州)如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O与点D,过点D的切线分别交AB、AC的延长线与点E、F.
(2013•随州)如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O与点D,过点D的切线分别交AB、AC的延长线与点E、F.(1)求证:AF⊥EF.
(2)小强同学通过探究发现:AF+CF=AB,请你帮忙小强同学证明这一结论.
分析:(1)首先连接OD,由EF是⊙O的切线,可得OD⊥EF,由∠BAC的平分线交⊙O与点D,易证得OD⊥BC,即可得BC∥EF,由AB为直径,根据直径所对的圆周角是直角,可得AC⊥BC,继而证得AF⊥EF.
(2)首先连接BD并延长,交AF的延长线于点H,连接CD,易证得△ADH≌△ADB,△CDF≌△HDF,继而证得AF+CF=AB.
(2)首先连接BD并延长,交AF的延长线于点H,连接CD,易证得△ADH≌△ADB,△CDF≌△HDF,继而证得AF+CF=AB.
解答: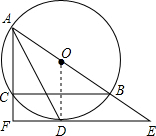 证明:(1)连接OD,
证明:(1)连接OD,
∵EF是⊙O的切线,
∴OD⊥EF,
∵AD平分∠BAC,
∴∠CAD=∠BAD,
∴
=
,
∴OD⊥BC,
∴BC∥EF,
∵AB为直径,
∴∠ACB=90°,
即AC⊥BC,
∴AF⊥EF;
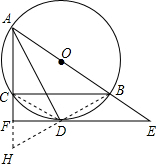 (2)连接BD并延长,交AF的延长线于点H,连接CD,
(2)连接BD并延长,交AF的延长线于点H,连接CD,
∵AB是直径,
∴∠ADB=90°,
即AD⊥BH,
∴∠ADB=∠ADH=90°,
在△ABD和△ADH中,
,
∴△ABD≌△AHD(ASA),
∴AH=AB,
∵EF是切线,
∴∠CDF=∠CAD,∠HDF=∠EDB=∠BAD,
∴∠CDF=∠HDF,
∵DF⊥AF,DF是公共边,
∴△CDF≌△HDF(ASA),
∴FH=CF,
∴AF+CF=AF+FH=AH=AB.
即AF+CF=AB,
 证明:(1)连接OD,
证明:(1)连接OD,∵EF是⊙O的切线,
∴OD⊥EF,
∵AD平分∠BAC,
∴∠CAD=∠BAD,
∴
 |
| CD |
 |
| BD |
∴OD⊥BC,
∴BC∥EF,
∵AB为直径,
∴∠ACB=90°,
即AC⊥BC,
∴AF⊥EF;
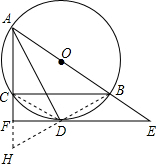 (2)连接BD并延长,交AF的延长线于点H,连接CD,
(2)连接BD并延长,交AF的延长线于点H,连接CD,∵AB是直径,
∴∠ADB=90°,
即AD⊥BH,
∴∠ADB=∠ADH=90°,
在△ABD和△ADH中,
|
∴△ABD≌△AHD(ASA),
∴AH=AB,
∵EF是切线,
∴∠CDF=∠CAD,∠HDF=∠EDB=∠BAD,
∴∠CDF=∠HDF,
∵DF⊥AF,DF是公共边,
∴△CDF≌△HDF(ASA),
∴FH=CF,
∴AF+CF=AF+FH=AH=AB.
即AF+CF=AB,
点评:此题考查了切线的性质、弦切角定理、圆周角定理以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
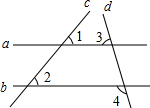 (2013•随州)如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是( )
(2013•随州)如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是( )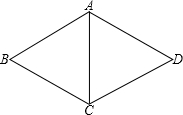 (2013•随州)如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是15,则菱形ABCD的周长是( )
(2013•随州)如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是15,则菱形ABCD的周长是( )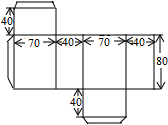 (2013•随州)如图是一个长方体形状包装盒的表面展开图.折叠制作完成后得到长方体的容积是(包装材料厚度不计)( )
(2013•随州)如图是一个长方体形状包装盒的表面展开图.折叠制作完成后得到长方体的容积是(包装材料厚度不计)( )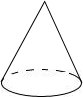 (2013•随州)如图是一圆锥,在它的三视图中,既是中心对称图形,又是轴对称图形的是它的
(2013•随州)如图是一圆锥,在它的三视图中,既是中心对称图形,又是轴对称图形的是它的