题目内容
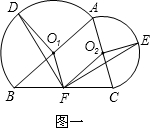
如图一,在△ABC中,分别以AB,AC为直径在△ABC外作半圆 和半圆
和半圆 ,其中
,其中 和
和 分别为两个半圆的圆心. F是边BC的中点,点D和点E分别为两个半圆圆弧的中点.
分别为两个半圆的圆心. F是边BC的中点,点D和点E分别为两个半圆圆弧的中点. 
(1)连结
 ,证明:
,证明: ;
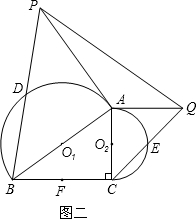
;(2)如图二,过点A分别作半圆
 和半圆
和半圆 的切线,交BD的延长线和CE的延长线于点P和点Q,连结PQ,若∠ACB=90°,DB=5,CE=3,求线段PQ的长;
的切线,交BD的延长线和CE的延长线于点P和点Q,连结PQ,若∠ACB=90°,DB=5,CE=3,求线段PQ的长;
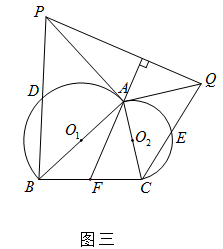
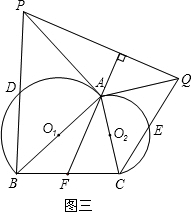
(3)如图三,过点A作半圆
 的切线,交CE的延长线于点Q,过点Q作直线FA的垂线,交BD的延长线于点P,连结PA. 证明:PA是半圆
的切线,交CE的延长线于点Q,过点Q作直线FA的垂线,交BD的延长线于点P,连结PA. 证明:PA是半圆 的切线
的切线
(1)证明略
(2)

(3)证明略解析:
(1)证明:如图一,∵
 ,
, ,F分别是AB,AC,BC边的中点,
,F分别是AB,AC,BC边的中点,
∴
 F∥AC且
F∥AC且 F =A
F =A ,
, F∥AB且
F∥AB且 F =A
F =A ,
,∴∠B
 F=∠BAC,∠C
F=∠BAC,∠C F=∠BAC,
F=∠BAC,∴∠B
 F=∠C
F=∠C F
F∵点D和点E分别为两个半圆圆弧的中点,
∴
 F =A
F =A =
= E,
E, F =A
F =A =
= D, ……………………….2分
D, ……………………….2分∠B
 D =90°,∠C
D =90°,∠C E =90°,
E =90°,∴∠B
 D=∠C
D=∠C E.
E.∴∠D
 F=∠F
F=∠F E.
E.∴
 . ………………………….3分
. ………………………….3分(2)解:如图二,延长CA至G,使AG=AQ,连接BG、AE.

∵点E是半圆
 圆弧的中点,
圆弧的中点,∴AE=CE=3
∵AC为直径
∴∠AEC=90°,
∴∠ACE=∠EAC =45°,AC=
 =
= ,
,∵AQ是半圆
 的切线,
的切线,∴CA⊥AQ,∴∠CAQ=90°,
∴∠ACE=∠AQE=45°,∠GAQ="90°"
∴AQ=AC=AG=

同理:∠BAP=90°,AB=AP=

∴CG=
 ,∠GAB=∠QAP
,∠GAB=∠QAP∴
 . ……………………..5分
. ……………………..5分∴PQ=BG
∵∠ACB=90°,
∴BC=
 =
=
∴BG=
 =
=
∴PQ=
 . …………………..6分
. …………………..6分(3) 证法一:如图三,设直线FA与PQ的垂足为M,过C作CS⊥MF于S,过B作BR⊥MF于R,连接DR、AD、DM.

∵F是BC边的中点,∴
 .
.∴BR=CS,
由(2)已证∠CAQ="90°," AC=AQ,
∴∠2+∠3=90°
∵FM⊥PQ, ∴∠2+∠1=90°,
∴∠1=∠3,
同理:∠2=∠4,
∴
 ,
,∴AM=CS,
∴AM=BR,
同(2)可证AD=BD,∠ADB=∠ADP=90°,
∴∠ADB=∠ARB="90°," ∠ADP=∠AMP=90°
∴A、D、B、R四点在以AB为直径的圆上,A、D、P、M四点在以AP为直径的圆上,
且∠DBR+∠DAR=180°,
∴∠5=∠8, ∠6=∠7,
∵∠DAM+∠DAR=180°,
∴∠DBR=∠DAM
∴
 ,
,∴∠5=∠9,
∴∠RDM=90°,
∴∠5+∠7=90°,
∴∠6+∠8=90°,
∴∠PAB=90°,
∴PA⊥AB,又AB是半圆
 直径,
直径,∴PA是半圆
 的切线. ……………………..8分
的切线. ……………………..8分证法二:假设PA不是是半圆
 的切线,如图四,
的切线,如图四,
过点A作半圆
 的切线交BD的延长线于点
的切线交BD的延长线于点 ,则点
,则点 异于点P,连结
异于点P,连结 ,设直线FA与PQ的垂足为M,直线FA与
,设直线FA与PQ的垂足为M,直线FA与 的交点为
的交点为 .延长AF至N,使得AF=FN,连结BN,CN,由于点F是BC中点,所以四边形ABNC是平行四边形.
.延长AF至N,使得AF=FN,连结BN,CN,由于点F是BC中点,所以四边形ABNC是平行四边形.易知,
 ,
,∵AQ是半圆
 的切线,
的切线,∴∠QAC=90°,同理
 .
.∴
 .
.∴
 .
.由(2)可知,
 ,
,∴
 .
.∴
 .
.∵
 ,
,∴
 .
.即
 .
.∴
 .
.即
 .
.∵
 ,
,∴ 过点Q有两条不同的直线
 和
和 同时与AF垂直.
同时与AF垂直.这与在平面内过一点有且仅有一条直线与已知直线垂直相矛盾,
因此假设错误.所以PA是是半圆
 的切线.
的切线. 
练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目



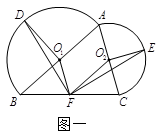


 和半圆
和半圆 ,其中
,其中 ,证明:
,证明: ;
;