题目内容
有一种产品，生产x吨需费用（1000+5x+| 1 |
| 10 |
| x |
| b |
分析：首先设出售x吨时，利润是y元，根据题意表示出利润，然后根据二次函数求最值方法进行计算，求出a，b．
解答：解：设出售x吨时，利润是y元，
则 y=(a+
)x-(1000+5x+
)
=
x2+(a-5)x-1000
依题意可知，
当x=150时，y有最大值，
则 a+
=40
当b＜0或b＞10时，
＜0，
故
=150②
∴
，
解①②得：
．
则 y=(a+
| x |
| b |
| x2 |
| 10 |
=
| 10-b |
| 10b |
依题意可知，
当x=150时，y有最大值，
则 a+
| 150 |
| b |
当b＜0或b＞10时，
| 10-b |
| 10b |
故
| 5b(a-5) |
| b-10 |
∴
|
解①②得：
|
点评：此题考查了函数模型的应用，通过对实际问题分析，转化为函数表达式，通过二次函数求最值计算，属于中档题．
练习册系列答案
步步高达标卷系列答案
相关题目
x2）元，而卖出x吨的价格为p元/吨，其中p=a+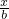
（a，b为常数），如果生产出来的产品全部卖掉，并且当产量是150吨时，所获利润最大，这时的价格为每吨40元，试求a，b的值．
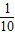x2）元，而卖出x吨的价格为p元/吨，其中p=a+
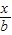（a，b为常数），如果生产出来的产品全部卖掉，并且当产量是150吨时，所获利润最大，这时的价格为每吨40元，则a，b的值分别为 、 ．
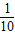x2）元，而卖出x吨的价格为p元/吨，其中p=a+
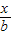（a，b为常数），如果生产出来的产品全部卖掉，并且当产量是150吨时，所获利润最大，这时的价格为每吨40元，试求a，b的值．