题目内容
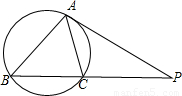
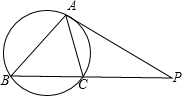 如图,P为圆外一点,PA切圆于A,PA=8,直线PCB交圆于C、B,且PC=4,连接AB、AC,∠ABC=α,∠ACB=β,则
如图,P为圆外一点,PA切圆于A,PA=8,直线PCB交圆于C、B,且PC=4,连接AB、AC,∠ABC=α,∠ACB=β,则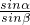 =________.
=________.

分析:过A作AD⊥BC于D,则得到三角形ABD和ACD为直角三角形,然后由角P为公共角,根据弦切角等于夹弧所对的圆周角得到角CAP等于角B,由两组对应角相等得到两三角形相似,得到对应边成比例,根据锐角三角函数定义表示出sinα和sinβ的比值,将已知的PA和PC的长代入即可求出值.
解答:
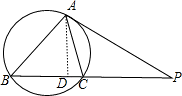 解:作AD⊥BC于D.则sinα=
解:作AD⊥BC于D.则sinα=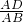 ,sinβ=
,sinβ=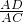 ,
,∵∠P=∠P,∠CAP=∠B,
∴△ACP∽△BAP,∴
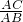 =
=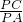 ,又PA=8,PC=4,
,又PA=8,PC=4,则
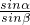 =
=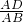 ÷
÷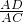 =
=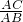 =
=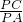 =
= ;
;故答案是:
 .
.点评:此题切线的性质,三角形相似的判别与性质,以及锐角三角函数的定义.作出AD垂直于BC构造两直角三角形是解本题的关键.解答此类题的方法是仔细审题,结合图形,找到突破点.

练习册系列答案
相关题目
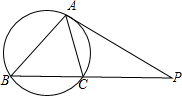 如图,P为圆外一点,PA切圆于A,PA=8,直线PCB交圆于C、B,且PC=4,连接AB、AC,∠ABC=α,∠ACB=β,则
如图,P为圆外一点,PA切圆于A,PA=8,直线PCB交圆于C、B,且PC=4,连接AB、AC,∠ABC=α,∠ACB=β,则 = .
= .
 =
.
=
.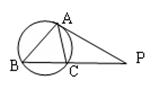
 = .
= .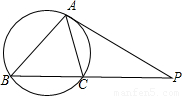
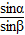 = .
= .