Question

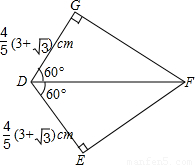
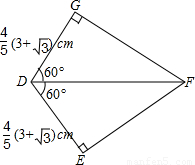
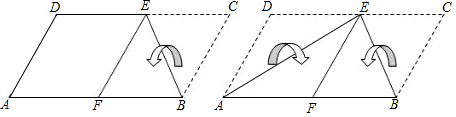
如图，一张四边形纸片ABCD，AD∥BC，将∠ABC对折使BC落在AB上，点C落在AB上点F处，此时我们可得到△BCE≌△BFE，再将纸片沿AE对折，D点刚好也落在点F上，由此我们又可得到一些结论，下述结论你认为正确的有
①AD=AF；②DE=EF=EC；③AD+BC=AB；④EF∥BC∥AD；⑤∠AEB=90°；⑥S_{四边形ABCD}=AE•BE

1. A.
   3个
2. B.
   4个
3. C.
   5个
4. D.
   6个

Answer 1

C
分析：根据翻折变换的性质易证AD=AF；DE=EF=EC；AD+BC=AB；∠AEB=90°；再根据直角三角形的面积公式易证S_{四边形ABCD}=2S_三角形AFB=AE•BE．
解答：①由于将纸片沿AE对折，D点刚好也落在点F上，∴AD=AF，故正确；
②由于将∠ABC对折使BC落在AB上，点C落在AB上点F处，∴DE=EF；由于将纸片沿AE对折，D点刚好也落在点F上，∴DE=EF，∴DE=EF=EC，故正确；
③由于将∠ABC对折使BC落在AB上，点C落在AB上点F处，∴BC=BF；∵AD=AF，∴AD+BC=AF+BF=AB，故正确；
④无法证明EF∥BC∥AD，故错误；
⑤∵∠DEF=2∠FEA，∠CEF=2∠FEB，∠DEC是平角，∴∠AEB=∠FEA+∠FEB=（∠DEF+∠CEF）=90°，∴∠AEB=90°，故正确；
⑥∵S_三角形ADE=S_三角形AFE，S_三角形BCE=S_三角形BFE，∴S_{四边形ABCD}=2S_三角形AFB=2×（AE•BE）=AE•BE，故正确．
故选C．
点评：本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等，对应线段相等．