题目内容
图1是棱长为a的小正方体,图2,图3由这样的小正方体摆放而成,按照这样的方法继续摆放,自上而下分别叫第一层,第二层,…第n层,第n层的小正方体的个数记为s,解答下列问题: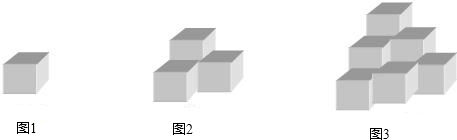
(1)按照要求填表:
| n | 1 | 2 | 3 | 4 | … |
| s | 1 | 3 | 6 | … |
(3)据上表中的数据,把s作为纵坐标,n作为横坐标,n作为横坐标,在平面直角坐标系中描出相应的各点.
(4)请你猜一猜上述各点会在某一个函数图象上吗?如果在某一函数的图象上,求出该函数的解析式.
分析:(1)找规律:s=1+2+3+…+n=
n(n+1);
(2)当n=10时,代入(1)中计算;
(3)描点;
(4)猜想,验证.
| 1 |
| 2 |
(2)当n=10时,代入(1)中计算;
(3)描点;
(4)猜想,验证.
解答:解:(1)由题意得
(2)当n=10时,s=
×10×(10+1)=55
(3)
(4)各点在二次函数的图象上.设函数的解析式为s=an2+bn+c,
由题意得
解之得
所以s=
n2+
n.
| n | 1 | 2 | 3 | 4 | … |
| s | 1 | 3 | 6 | 10 |
| 1 |
| 2 |
(3)

(4)各点在二次函数的图象上.设函数的解析式为s=an2+bn+c,
由题意得
|
解之得
|
所以s=
| 1 |
| 2 |
| 1 |
| 2 |
点评:找规律是本题关键,猜想函数关系式后需验证.

练习册系列答案
相关题目
 18、如图,把一个棱长为3的正方体的每个面等分成9个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去了7个小正方体),所得到的几何体的表面积是
18、如图,把一个棱长为3的正方体的每个面等分成9个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去了7个小正方体),所得到的几何体的表面积是 11、如图,把一个棱长为3的正方体的每个面等分成9个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去7个小正方体),所得到的几何体的表面积是( )
11、如图,把一个棱长为3的正方体的每个面等分成9个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去7个小正方体),所得到的几何体的表面积是( ) 平面图形相似的概念可以推广到空间立体图形.例如:任意两个球体都是相似的;任意两个正方体都是相似的;等等.立体相似也有平面相似图形相类似的性质.
平面图形相似的概念可以推广到空间立体图形.例如:任意两个球体都是相似的;任意两个正方体都是相似的;等等.立体相似也有平面相似图形相类似的性质. 如图,把一个棱长为3的正方体的每个面等分成9个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去7个小正方体),所得到的几何体的表面积是( )
如图,把一个棱长为3的正方体的每个面等分成9个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去7个小正方体),所得到的几何体的表面积是( )
 B.
B. C.
C. D.
D. 