题目内容
如图，⊙O的两弦AB，CD互相垂直于H，AH=4，BH=6，CH=3，DH=8，求⊙O的半径．
【答案】分析：过O分别作OM⊥AB于M，ON⊥CD于N，得矩形MHNO，连BO．由垂径定理求出MO、MB，再由勾股定理求得BO的长．
解答：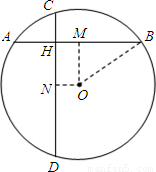
解：过O分别作OM⊥AB于M，ON⊥CD于N，得矩形MHNO，连接BO．
根据垂径定理得到：M为AB中点，N为CD中点，
∴MO=NH=CN-CH=
CD-CH=
（CH+HD）-CH，
∴MO=（8-3）÷2=
，
∵MB=
AB=
（AH+BH），
∴MB=5，
∴Rt△BOM中，
BO=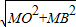
=
．
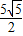故答案为：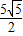
．
点评：本题考查了勾股定理和垂径定理，解答这类题一些学生不会综合运用所学知识解答问题，不知从何处入手造成错解．
解答：
解：过O分别作OM⊥AB于M，ON⊥CD于N，得矩形MHNO，连接BO．根据垂径定理得到：M为AB中点，N为CD中点，
∴MO=NH=CN-CH=
CD-CH=（CH+HD）-CH，∴MO=（8-3）÷2=
，∵MB=
AB=（AH+BH），∴MB=5，
∴Rt△BOM中，
BO=
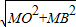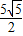=．故答案为：
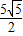．点评：本题考查了勾股定理和垂径定理，解答这类题一些学生不会综合运用所学知识解答问题，不知从何处入手造成错解．
练习册系列答案
相关题目
如图，⊙O的两弦AB，CD互相垂直于H，AH=4，BH=6，CH=3，DH=8，求⊙O的半径．
8、如图，⊙O的两弦AB、CD相交于点M，AB=8cm，M是AB的中点，CM：MD=1：4，则CD=（ ）
如图，⊙O的两弦AB，CD互相垂直于H，AH=4，BH=6，CH=3，DH=8，求⊙O的半径．