题目内容
如图,将等边三角形PQR放在正方形ABCD上,边QR与AB完全重合.则:(1)图①中点P与正方形中的任意两个顶点能构成多少个等腰三角形(等边△PQR除外)?直接写出这些三角形的名称
(2)现在将正方形ABCD固定不动,等边三角形PQR绕着点R旋转,使点P与C重合(如图②,这算第1步,点P落在P1处),再绕着点P旋转,使点Q与点D重合(如图③,这算第2步,点P落在P2处),重复这样的步骤,可得到图④…,则请你探究:经过
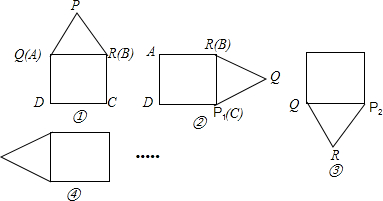
(3)若正方形ABCD的边长等于4,则按第(2)题的方法从图①开始,连续旋转了2006步,最后点P落在P2006处.请画出此时图形的位置,并计算此时点P2006到RA的距离.
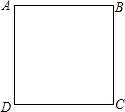
分析:(1)根据等腰三角形的性质,两条边相等的三角形为等腰三角形,从而可以得出△PAD,△PCD,△PBC为等腰三角形;
(2)从图中的例子找出规律,即经过4步三角形回到原处,但是对应顶点变换一次,可知共有三个顶点,当经过12次时,对应顶点回到原处;
(3)因为点P每过12步回到原位置,可以通过(2)中规律知道经过2006步点P所在的位置,从而根据三角函数可以得出P2006到RA的距离.
(2)从图中的例子找出规律,即经过4步三角形回到原处,但是对应顶点变换一次,可知共有三个顶点,当经过12次时,对应顶点回到原处;
(3)因为点P每过12步回到原位置,可以通过(2)中规律知道经过2006步点P所在的位置,从而根据三角函数可以得出P2006到RA的距离.
解答: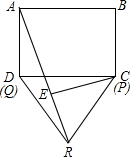 解:(1)根据等腰三角形的性质△PAD,△PCD,△PBC为等腰三角形
解:(1)根据等腰三角形的性质△PAD,△PCD,△PBC为等腰三角形
∵PA=AD,∴△PAD为等腰三角形;
∵PB=BC,∴△PBC为等腰三角形;
∵△PAD≌△PBC,∴PD=PC,
∴△PCD为等腰三角形.
(2)从图中可以得到以下规律,经过4步三角形回到原处,但是对应顶点变换一次,可知共有三个顶点,当经过12次时,对应顶点回到原处;
(3)从第(2)问中的规律可以知道第2006步时,点P应该在如图所示的位置,与点C重合
作CE垂直于AR,从正方形ABCD和等边三角形PQR的性质可以得出
∠ADR=90°+60°=150°,
∵AD=DR∴∠ARD=15°,
∴∠ECR=60°-15°=45°,
∵CE⊥AR,CR=AB=4,
∴在等腰直角△CER中应用勾股定理
CE=2
.
 解:(1)根据等腰三角形的性质△PAD,△PCD,△PBC为等腰三角形
解:(1)根据等腰三角形的性质△PAD,△PCD,△PBC为等腰三角形∵PA=AD,∴△PAD为等腰三角形;
∵PB=BC,∴△PBC为等腰三角形;
∵△PAD≌△PBC,∴PD=PC,
∴△PCD为等腰三角形.
(2)从图中可以得到以下规律,经过4步三角形回到原处,但是对应顶点变换一次,可知共有三个顶点,当经过12次时,对应顶点回到原处;
(3)从第(2)问中的规律可以知道第2006步时,点P应该在如图所示的位置,与点C重合
作CE垂直于AR,从正方形ABCD和等边三角形PQR的性质可以得出
∠ADR=90°+60°=150°,
∵AD=DR∴∠ARD=15°,
∴∠ECR=60°-15°=45°,
∵CE⊥AR,CR=AB=4,
∴在等腰直角△CER中应用勾股定理
CE=2
| 2 |
点评:了解等腰三角形的判定定理,根据题中所给的图形找出规律是做题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
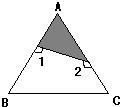
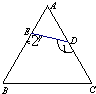 12、如图,将等边三角形纸片(△ABC)的∠A剪下,则∠1+∠2=
12、如图,将等边三角形纸片(△ABC)的∠A剪下,则∠1+∠2=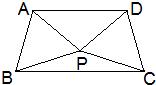 22、如图,将等边三角形APB绕顶点P按顺时针方向旋转150°后,得到△CPD,连接AD、BC.
22、如图,将等边三角形APB绕顶点P按顺时针方向旋转150°后,得到△CPD,连接AD、BC.