Question

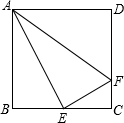
已知，如图，Rt△ABC中，∠ACB=90°，AB=5，两直角边AC、BC的长是关于x的方程x²-（m+5）x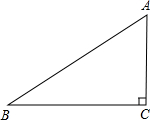+6m=0的两个实数根．
（1）求m的值及AC、BC的长（BC＞AC）；
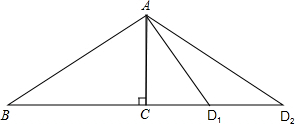
（2）在线段BC的延长线上是否存在点D，使得以D、A、C为顶点的三角形与△ABC相似？若存在，求出CD的长；若不存在，请说明理由．

Answer 1

（1）设方程x²-（m+5）x+6m=0的两个根分别是x₁、x₂
∴x₁+x₂=m+5，x₁•x₂=6m
∴x₁²+x₂²=（x₁+x₂）²-2x₁x₂=（m+5）²-2×6m
∵Rt△ABC中，∠ACB=90°，AB=5
∴x₁²+x₂²=AB²
∴（m+5）²-2×6m=5²∴m²-2m=0
∴m=0或m=2
当m=0时，原方程的解分别为x₁=0，x₂=5，但三角形的边长不能为0，所以m=0舍去．
当m=2时，原方程为x²-7x+12=0，其解为x₁=3，x₂=4，所以两直角边AC=3，BC=4
∴m=2，AC=3，BC=4

（2）存在；
已知AC=3，BC=4，AB=5
欲使以△AD₁C为顶点的三角形与△ABC相似，则

AB

AD1

=

AC

CD1

=

BC

AC

，∴

3

CD1

=

4

3

，则CD=

9

4

欲使以△AD₂C为顶点的三角形与△ABC相似，则

AB

AD2

=

BC

CD2

=

AC

AC

，∴BC=CD₂=4