题目内容
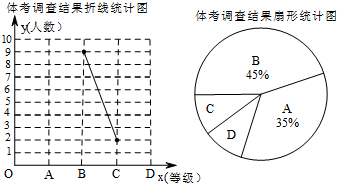
我校初三学子在不久前结束的体育中考中取得满意成绩，赢得2013年中考开门红．现随机抽取了部分学生的成绩作为一个样本，按A（满分）、B（优秀）、C（良好）、D（及格）四个等级进行统计，并将统计结果制成如下2幅不完整的统计图，如图，请你结合图表所给信息解答下列问题：
（1）此次调查共随机抽取了??????? 名学生，其中学生成绩的中位数落在??????? 等级；
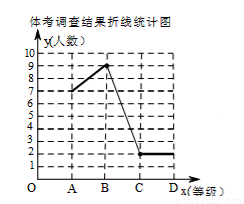
（2）将折线统计图在图中补充完整；
（3）为了今后中考体育取得更好的成绩，学校决定分别从成绩为满分的男生和女生中各选一名参加“经验座谈会”，若成绩为满分的学生中有4名女生，且满分的男、女生中各有2名体育特长生，请用列表或画树状图的方法求出所选的两名学生刚好都不是体育特长生的概率．
（1）20，B；（2）补全图形见解析；（3）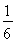
.
【解析】
试题分析：（1）根据B的人数及所占的比例，可得出调查的学生总数，分别求出A、C、D的人数后可得出学生成绩的中位数落在哪个等级；
（2）根据各等级的人数，补全折线统计图即可；
（3）列出表格，根据概率公式计算即可．
试题解析：（1）共抽取的学生人数为：9÷45%=20人，
∵A等级有20×35%=7人，D等级有20-7-9-2=2人，
∴按照成绩从高到低，第10、11两人都在B等级，
∴中位数在B等级；
（2）A等级人数有7人，B等级人数为9人，C等级人数为2人，D等级人数为2人，
补全条形统计图如图；
（3）成绩为满分的四名女生分别为女1，女2，女3，女4，其中女1，女2是体育特长生；
成绩为满分的三名男生为男1，男2，男3，其中男1，男2是体育特长生；
列出如下：
| 女1 | 女2 | 女3 | 女4 |
男1 | （男1，女1） | （男1，女2） | （男1，女3） | （男1，女4） |
男2 | （男2，女1） | （男2，女2） | （男2，女3） | （男2，女4） |
男3 | （男3，女1） | （男3，女2） | （男3，女3） | （男3，女4） |
由表可得共有12种情况，其中都不是体育特长生的有2种情况，
所以P（都不是体育特长生）=
．
考点: 1.折线统计图；2.扇形统计图；3.列表法与树状图法.
