题目内容
若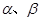 是一元二次方程
是一元二次方程 的实根,且满足
的实根,且满足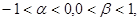 则
则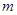 的取值范围是________
的取值范围是________
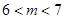
解析考点:一元二次方程根的分布.
分析:根据题意知:当m>0时,m-7<0,m<7,且f(-1)>0,f(1)>0,求出m的取值范围,同理求出当m<0,满足条件的m的取值范围.
解:α、β是一元二次方程mx2-(m-1)x+m-7=0的实根,-1<α<0,0<β<1,
令y=mx2-(m-1)x+m-7,
当m>0时,函数图象的开口向上,图象与y轴负半轴有交点,即m-7<0,m<7,
且f(-1)>0,f(1)>0,
解得m>6,即6<m<7,
当m<0,函数图象的开口向下,图象与y轴正半轴有交点则m-7>0,
m不存在,
综上6<m<7,
故答案为6<m<7.

练习册系列答案
相关题目
 是一元二次方程
是一元二次方程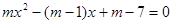 的实根,且满足
的实根,且满足 则
则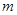 的取值范围是________
的取值范围是________ 是一元二次方程
是一元二次方程 的实根,且满足
的实根,且满足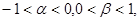 则
则 的取值范围是________
的取值范围是________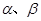 是一元二次方程
是一元二次方程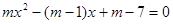 的实根,且满足
的实根,且满足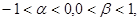 则
则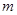 的取值范围是________
的取值范围是________