题目内容
反比例函数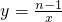
的图象在第二、四象限，则n的取值范围为________，A（2，y1），B（3，y2）为图象上两点，则y1________y2（用“＜”或“＞”填空）．
n＜1 ＜
分析：根据反比例函数的性质再结合反比例函数图象上点的坐标特征即可求解．
解答：因为反比例函数y=
的图象在第二、四象限，
所以n-1＜0，
所以n＜1．
又因为A（2，y1），B（3，y2）在第四象限，
所以y1＜y2．
故答案为：n＜1，＜．
点评：反比例函数图象上点的坐标特征：当k＞0时，图象分别位于第一、三象限，横纵坐标同号；当k＜0时，图象分别位于第二、四象限，横纵坐标异号．
分析：根据反比例函数的性质再结合反比例函数图象上点的坐标特征即可求解．
解答：因为反比例函数y=
的图象在第二、四象限，所以n-1＜0，
所以n＜1．
又因为A（2，y1），B（3，y2）在第四象限，
所以y1＜y2．
故答案为：n＜1，＜．
点评：反比例函数图象上点的坐标特征：当k＞0时，图象分别位于第一、三象限，横纵坐标同号；当k＜0时，图象分别位于第二、四象限，横纵坐标异号．
练习册系列答案
名校课堂系列答案
相关题目
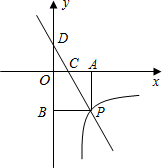如图，一次函数y=kx+3的图象分别交x轴、y轴于点C、点D，与反比例函数
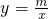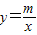的图象在第四象限的相交于点P，并且PA⊥x轴于点A，PB⊥y轴于点B，已知B（0，-6），且S△DBP=27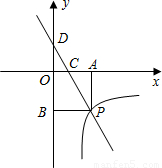
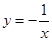的图象在第 象限．
的图象在第四象限的相交于点P，并且PA⊥x轴于点A，PB⊥y轴于点B，已知B（0，-6），且S△DBP=27
的图象在第
象限．