题目内容
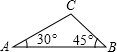
2006年6月某工厂将地处A，B两地的两个小工厂合成一个大厂，为了方便A，B两地职工的联系，企业准备在相距2km的A，B两地之间修一条笔直的公路（即图中的线段AB），经测量，在A地的北偏东60°方向，B地的西偏北45°方向的C处有一半径为0.7km的公园，则修筑的这条公路会不会穿过公园？为什么？
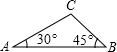
解：如图所示，过点C作CD⊥AB，垂足为D．
∵∠B=45°，
∴∠BCD=45°，CD=BD．
设CD=x，则BD=x；
由∠A=30°知AC=2x，AD=
=
x，
∴x+x=2，
（+1）x=2，
则x=
=
=-1；
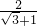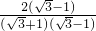即CD=-1≈0.732（km）＞0.7km．
也就是说，以C为圆心，以0.7km为半径的圆与AB相离．
答：计划修筑的这条公路不会穿过公园．
分析：要判断是否穿过公园，只需求得点C到AB的垂线段的长度，然后和半径进行比较即可．
点评：能够根据特殊角发现边之间的关系型，求得点C到直线的最短距离，然后和半径进行比较即可．
∵∠B=45°，
∴∠BCD=45°，CD=BD．
设CD=x，则BD=x；
由∠A=30°知AC=2x，AD=
=x，∴
x+x=2，（
+1）x=2，则x=
==-1；即CD=
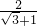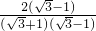-1≈0.732（km）＞0.7km．也就是说，以C为圆心，以0.7km为半径的圆与AB相离．
答：计划修筑的这条公路不会穿过公园．
分析：要判断是否穿过公园，只需求得点C到AB的垂线段的长度，然后和半径进行比较即可．
点评：能够根据特殊角发现边之间的关系型，求得点C到直线的最短距离，然后和半径进行比较即可．
练习册系列答案
阅读快车系列答案
相关题目
依法纳税是每个公民应尽的义务。《中华人民共和国个人所得税法》规定，公民每月收入不超过l600元，不需交税；超过l600元的部分为全月应纳税所得额，应纳税，且根据超过部分的多少按不同的税率纳税，详细的税率如下表：
(1)某工厂一名工人2006年5月的收入为2000元，问他应交税款多少元?
(2)设
表示公民每月收入(单位：元)，y表示应交税款(单位：元)，当2100≤≤3600时，请写出y关于的函数关系式；
(3)某公司一名职员2006年5月应交税款120元，问该月他的收入是多少元?
| 级别 | 全月应纳税所得额 | 税率(％) |
| l | 不超过500元的 | 5 |
| 2 | 超过500元至2000元的部分 | 10 |
| 3 | 超过2000元至5000元的部分 | 15 |
| … | … | … |
