题目内容
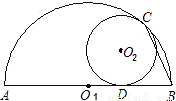
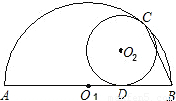
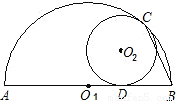
14、如图，⊙O2与半圆Ol内切于点C，与半圆的直径AB切于点D，若AB=6，⊙O2的半径为1，则∠ABC的度数为75
度．分析：连接O1C，O2D，AC．根据相切两圆的性质和圆周角定理求解．
解答：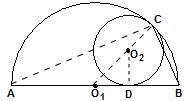
解：AB=6，则O1B=3．
连接O1C，则O1C一定经过点O2，则O1O2=3-1=2；
连接O2D．则O2D⊥O1B，O2D=1，因而∠O2O1B=30°；
连接AC，则∠CAB=15°，因而∠ABC的度数为75°．
解：AB=6，则O1B=3．连接O1C，则O1C一定经过点O2，则O1O2=3-1=2；
连接O2D．则O2D⊥O1B，O2D=1，因而∠O2O1B=30°；
连接AC，则∠CAB=15°，因而∠ABC的度数为75°．
点评：本题是一个综合题，综合运用了切线的性质，直径所对的圆周角是直角，相切的两圆的圆心以及切点在同一条直线上．
练习册系列答案
相关题目
