题目内容
如图，直线AB和DE相交于一点O，AB⊥CO，则∠COE与∠AOD一定
- A.互补
- B.互余
- C.相等
- D.是对顶角
B
分析：根据AB⊥CO，可知∠COE+∠BOE=90°，然后根据对顶角相等可知∠AOD=∠BOE，继而可得∠AOD+∠COE=90°，可判断∠AOD和∠COE互余．
解答：∵AB⊥CO，
∴∠COE+∠BOE=90°，
∵∠AOD和∠BOE是对顶角，
∴∠AOD=∠BOE，
则∠AOD+∠COE=90°，
即∠AOD和∠COE互余．
故选B．
点评：本题考查了余角的知识，解答本题的关键是熟练掌握互余两角之和为90°，属于基础题．
分析：根据AB⊥CO，可知∠COE+∠BOE=90°，然后根据对顶角相等可知∠AOD=∠BOE，继而可得∠AOD+∠COE=90°，可判断∠AOD和∠COE互余．
解答：∵AB⊥CO，
∴∠COE+∠BOE=90°，
∵∠AOD和∠BOE是对顶角，
∴∠AOD=∠BOE，
则∠AOD+∠COE=90°，
即∠AOD和∠COE互余．
故选B．
点评：本题考查了余角的知识，解答本题的关键是熟练掌握互余两角之和为90°，属于基础题．
练习册系列答案
相关题目
（2013•澄江县一模）如图，直线AB和DE相交于一点O，AB⊥CO，则∠COE与∠AOD一定（ ）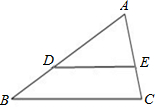
（1）已知△ABC中，D、E分别是边AB、AC上的点，∠A=80°，∠C=70°，∠ADE=30°．求证：DE∥BC．
