题目内容
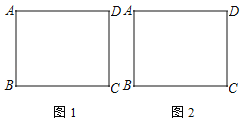
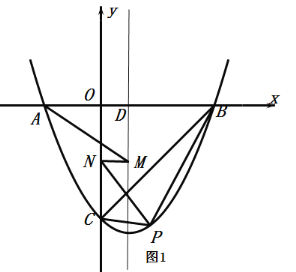
【题目】如图,正方形ABCD,将边BC绕点B逆时针旋转60°,得到线段BE,连接AE,CE.
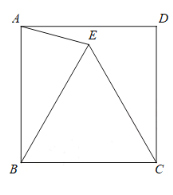
(1)求∠BAE的度数;
(2)连结BD,延长AE交BD于点F.
①求证:DF=EF;
②直接用等式表示线段AB,CF,EF的数量关系.
【答案】(1) 75°;(2)①见解析②![]()
【解析】
(1)根据题意利用等腰三角形性质以及等量代换求∠BAE的度数;
(2)①由正方形的对称性可知,∠DAF=∠DCF=15°,从而证明△BCF≌△ECF,求证DF=EF;
②题意要求等式表示线段AB,CF,EF的数量关系,利用等腰直角三角形以及等量代换进行分析.
(1)解:∵AB=BE,
∴∠BAE=∠BEA.
∵∠ABE=90°-60°=30°
∴∠BAE=75°.

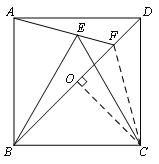

(2)①证明:∴∠DAF=15°.连结CF.
由正方形的对称性可知,∠DAF=∠DCF=15°.
∵∠BCD=90°,∠BCE=60°,
∴∠DCF=∠ECF=∠DAF=15°.
∵BC=EC,CF=CF,
∴△DCF≌△ECF.
∴DF=EF.
②过C作CO垂直BD交于O,

由题意求得∠OCF=30°,设OF=x,CF=2x,OB=OC=OD=![]() x,EF=DF=OD-OF=
x,EF=DF=OD-OF=![]() x-x则BC=AB=
x-x则BC=AB=![]() 有
有![]() 即有
即有![]() .
.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案【题目】二次函数![]() 上部分点的横坐标x与纵坐标y的对应值如下表:
上部分点的横坐标x与纵坐标y的对应值如下表:
x | … |
|
| 0 | 1 | 2 | 3 | … |
y | … | 3 |
| 0 |
| 0 | m | … |
(1)直接写出此二次函数的对称轴 ;
(2)求b的值;
(3)直接写出表中的m值,m= ;
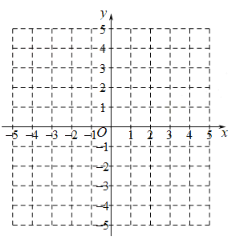
(4)在平面直角坐标系xOy中,画出此二次函数的图象.
【题目】已知甲、乙两家公司员工日工资情况:甲公司日工资是底薪100元,每完成一件产品工资计3元;乙公司无底薪,40件以内(含40件)产品的部分每件产品工资计8元,超出40件的部分每件产品工资计10元,为此,在这两家公司各随机调查了100名工人日完成产品数,并整理得到如下频数分布表:
日完成产品数 | 38 | 39 | 40 | 41 | 42 |
甲公司工人数 | 20 | 40 | 20 | 10 | 10 |
乙公司工人数 | 10 | 20 | 20 | 40 | 10 |
(1)若甲、乙公司日工资加上其他福利,总的待遇相同,A、B两人分别到甲、乙公司应聘,都选中甲公司的概率是多少?
(2)试以这两家公司各100名工人日工资的平均数作为决策依据,若某人要去这两家公司应聘,为他做出选择,去哪一家公司的经济收入可能会多一些?