题目内容
【题目】如图,直线y=![]() x+
x+![]() 与两坐标轴分别交于A、B两点.
与两坐标轴分别交于A、B两点.
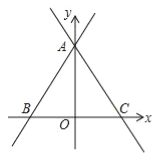
(1)求∠ABO的度数;
(2)过A的直线l交x轴半轴于C,AB=AC,求直线l的函数解析式.
【答案】(1)∠ABO=60°;(2)y=﹣![]() x+
x+![]() .
.
【解析】
试题分析:(1)根据一次函数解析式y=![]() x+
x+![]() 求出点A、B的坐标,在Rt△ABO中,求出tan∠ABO的值,从而求出∠ABO的度数;(2)根据题意可得,AB=AC,AO⊥BC,可得AO为BC的中垂线,根据点B的坐标,求得点C的坐标,利用待定系数法求出直线l的函数解析式即可.
求出点A、B的坐标,在Rt△ABO中,求出tan∠ABO的值,从而求出∠ABO的度数;(2)根据题意可得,AB=AC,AO⊥BC,可得AO为BC的中垂线,根据点B的坐标,求得点C的坐标,利用待定系数法求出直线l的函数解析式即可.
试题解析:(1)对于直线y=![]() x+
x+![]() ,
,
令x=0,则y=![]() ,
,
令y=0,则x=﹣1,
故点A的坐标为(0,![]() ),点B的坐标为(﹣1,0),
),点B的坐标为(﹣1,0),
则AO=![]() ,BO=1,
,BO=1,
在Rt△ABO中,
∵tan∠ABO=![]() =
=![]() ,
,
∴∠ABO=60°;
(2)在△ABC中,
∵AB=AC,AO⊥BC,
∴AO为BC的中垂线,
即BO=CO,
则C点的坐标为(1,0),
设直线l的解析式为:y=kx+b(k,b为常数),
则![]() ,
,
解得:![]() ,
,
即函数解析式为:y=﹣![]() x+
x+![]() .
.

练习册系列答案
相关题目