Question

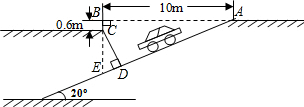
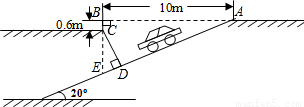
随着私家车的逐渐增多，居民小区“停车难”问题日益突出．本市某居民小区为缓解“停车难”问题，小区物业部门拟建造一个新的地下停车库．建筑设计师提供了该地下停车库设计图（如图）．按规定，地下停车库坡道口上方要张贴限高标志，以便告知停车人车辆能否驶入．为标明限高，请你根据该图计算CD（精确到0.1m）
（参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，cot20°≈2.75）

Answer 1

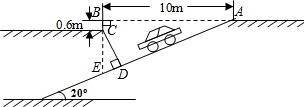
分析：根据锐角三角函数的定义，可在Rt△ABE中解得BE的值，进而求得CE的大小；在Rt△CDE中，利用正弦的定义，即可求得CD的值．

解答：解：在△ABE中，∠ABE=90°，∠BAE=20°…（1分）
∴tan∠BAE=

BE

AB

，又AB=10，
∴BE=AB•tan∠BAE=10tan20°≈3.6m，…（2分）
∵BC=0.6∴CE=BE-BC=3m  …（1分）
在△CED中，∵CD⊥AE，∠ECD=∠BAE=20°…（1分）
∴cos∠ECD=

CD

CE

…（1分）
∴CD=CE•cos∠ECD=3cos20°≈3×0.94≈2.8m．
故答案为2.8m．

点评：此题考查了三角函数的基本概念，主要是正弦、正切概念及运算，关键把实际问题转化为数学问题加以计算．利用三角函数首先要确定直角三角形．