题目内容
(1999•河北)若菱形的周长为16,两邻角度数之比为1:2,则该菱形的面积为( )A.4
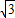
B.8

C.10
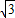
D.12
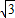
【答案】分析:根据“两邻角度数之比为1:2”求出菱形的内角,再根据周长求出边长,所以两对角线的长度可求,利用菱形的面积等于对角线乘积的一半即可求解.
解答: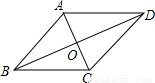 解:如图,∵两邻角度数之比为1:2,两邻角和为180°,
解:如图,∵两邻角度数之比为1:2,两邻角和为180°,
∴∠ABC=60°,∠BAD=120°,
∵周长为16,
∴边长AB=4,
∴菱形的对角线AC=4,BD=2×4sin60°=4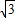 ,
,
∴面积= AC•BD=
AC•BD= ×4×4
×4×4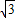 =8
=8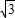 .
.
故选B.
点评:本题求出菱形的一个内角是60°是求两对角线的关键,利用对角线乘积的一半求菱形的面积需要熟练掌握.
解答:
 解:如图,∵两邻角度数之比为1:2,两邻角和为180°,
解:如图,∵两邻角度数之比为1:2,两邻角和为180°,∴∠ABC=60°,∠BAD=120°,
∵周长为16,
∴边长AB=4,
∴菱形的对角线AC=4,BD=2×4sin60°=4
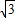 ,
,∴面积=
 AC•BD=
AC•BD= ×4×4
×4×4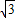 =8
=8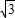 .
.故选B.
点评:本题求出菱形的一个内角是60°是求两对角线的关键,利用对角线乘积的一半求菱形的面积需要熟练掌握.

练习册系列答案
相关题目