题目内容
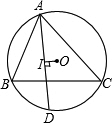
如图，不等边△ABC内接于⊙O，I是其内心，且AI⊥OI．
求证：AB+AC=2BC．
证明：延长AI交⊙O于D，连接OA、OD、BD和BI，
∵OA=OD，OI⊥AD，
∴AI=ID，
又∠DBI=∠DBC+∠CBI=∠DAC+∠CBI，
=
（∠BAC+∠ABC）=∠DIB，
因此，BD=ID=AI，
易证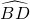
=
，
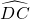故OD⊥BC，记垂足为E，则有BE=BC，
作IG⊥AB于G，又∠DBE=∠IAG，而BD=AI，
∴Rt△BDE≌Rt△AIG，
于是，AG=BE=BC，但AG=（AB+AC-BC），
故AB+AC=2BC．
分析：延长AI交⊙O于D，连接OA、OD、BD和BI，可得BD=ID=AI．易证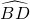=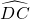，则OD⊥BC，作IG⊥AB于G，又∠DBE=∠IAG，则BD=AI，所以Rt△BDE≌Rt△AIG，从而得出AB+AC=2BC．
点评：本题考查了三角形的内切圆和全等三角形的判定和性质．
∵OA=OD，OI⊥AD，
∴AI=ID，
又∠DBI=∠DBC+∠CBI=∠DAC+∠CBI，
=
（∠BAC+∠ABC）=∠DIB，因此，BD=ID=AI，
易证
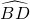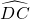=，故OD⊥BC，记垂足为E，则有BE=
BC，作IG⊥AB于G，又∠DBE=∠IAG，而BD=AI，
∴Rt△BDE≌Rt△AIG，
于是，AG=BE=
BC，但AG=（AB+AC-BC），故AB+AC=2BC．
分析：延长AI交⊙O于D，连接OA、OD、BD和BI，可得BD=ID=AI．易证
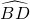=，则OD⊥BC，作IG⊥AB于G，又∠DBE=∠IAG，则BD=AI，所以Rt△BDE≌Rt△AIG，从而得出AB+AC=2BC．点评：本题考查了三角形的内切圆和全等三角形的判定和性质．
练习册系列答案
相关题目
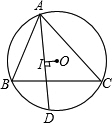
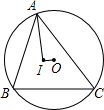如图，不等边△ABC内接于⊙O，I是其内心，且AI⊥OI．
