题目内容
某汽车在刹车后行驶的距离s(单位:米)与时间t(单位:秒)之间的关系得部分数据如下表:

(1)根据这些数据在给出的坐标系中画出相应的点;
(2)选择适当的函数表示s与t之间的关系,求出相应的函数解析式;
(3)①刹车后汽车行驶了多长距离才停止?
②当t分别为t1,t2(t1<t2)时,对应s的值分别为s1,s2,请比较 与
与 的大小,并解释比较结果的实际意义。
的大小,并解释比较结果的实际意义。
(2)选择适当的函数表示s与t之间的关系,求出相应的函数解析式;
(3)①刹车后汽车行驶了多长距离才停止?
②当t分别为t1,t2(t1<t2)时,对应s的值分别为s1,s2,请比较
 与
与 的大小,并解释比较结果的实际意义。
的大小,并解释比较结果的实际意义。
解:(1)描点图所示: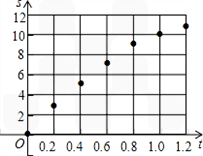
(2)由散点图可知该函数为二次函数设二次函数的解析式为:s=at2+bt+c,
∵抛物线经过点(0,0),
∴c=0,
又由点(0.2,2.8),(1,10)可得:
解得:a=﹣5,b=15;
∴二次函数的 解析式为:s=﹣5t2+15t;
解析式为:s=﹣5t2+15t;
经检验,其余个点均在s=﹣5t2+15t上; (3)①汽车刹车后到停止时的距离即汽车滑行的最大距离,
(3)①汽车刹车后到停止时的距离即汽车滑行的最大距离,
当t=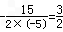 时, 滑行距离最大,
时, 滑行距离最大,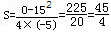
即刹车后汽车行驶了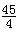 米才停止,
米才停止,
②∵s=﹣5t2+15t,
∴s1=﹣5t12+15t1,s2=﹣5t22+15t2
∴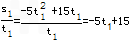
同理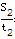 =﹣5t2+15,
=﹣5t2+15,
∴t1<t2,
∴ ,
,
其实际意义是刹车后到t2时间内的平均速到t1时间内的度小于刹车后平均速度。

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
某汽车在刹车后行驶的距离s(单位:米)与时间t(单位:秒)之间的关系得部分数据如下表:
| 时间t(秒) | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | … |
| 行驶距离s(米) | 0 | 2.8 | 5.2 | 7.2 | 8.8 | 10 | 10.8 | … |
(1)根据这些数据在给出的坐标系中画出相应的点;
(2)选择适当的函数表示s与t之间的关系,求出相应的函数解析式;
(3)①刹车后汽车行驶了多长距离才停止?
②当t分别为t1,t2(t1<t2)时,对应s的值分别为s1,s2,请比较![]() 与
与![]() 的大小,并解释比较结果的实际意义.
的大小,并解释比较结果的实际意义.

某汽车在刹车后行驶的距离s(单位:米)与时间t(单位:秒)之间的关系得部分数据如下表:
假设这种变化规律一直延续到汽车停止.
(1)根据这些数据在给出的坐标系中画出相应的点;
(2)选择适当的函数表示s与t之间的关系,求出相应的函数解析式;
(3)①刹车后汽车行驶了多长距离才停止?
②当t分别为t1,t2(t1<t2)时,对应s的值分别为s1,s2,请比较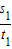 与
与 的大小,并解释比较结果的实际意义.
的大小,并解释比较结果的实际意义.

| 时间t(秒) | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | … | |
| 行驶距离s(米) | 2.8 | 5.2 | 7.2 | 8.8 | 10 | 10.8 | … |
(1)根据这些数据在给出的坐标系中画出相应的点;
(2)选择适当的函数表示s与t之间的关系,求出相应的函数解析式;
(3)①刹车后汽车行驶了多长距离才停止?
②当t分别为t1,t2(t1<t2)时,对应s的值分别为s1,s2,请比较
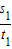 与
与 的大小,并解释比较结果的实际意义.
的大小,并解释比较结果的实际意义.
某汽车在刹车后行驶的距离s(单位:m)与时间t(单位:s)之间的关系得部分数据如下表:
|
时间t(s) |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
1.2 |
… |
|
行驶距离s(m) |
0 |
2.8 |
5.2 |
7.2 |
8.8 |
10 |
10.8 |
… |
假设这种变化规律一直延续到汽车停止.
(1)根据这些数据在给出的坐标系中画出相应的点;

(2)选择适当的函数表示s与t之间的关系,求出相应的函数解析式;
(3)刹车后汽车行驶了多长距离才停止?

 某汽车在刹车后行驶的距离s(单位:米)与时间t(单位:秒)之间的关系得部分数据如下表:
某汽车在刹车后行驶的距离s(单位:米)与时间t(单位:秒)之间的关系得部分数据如下表: