题目内容
(2011•陕西)2011年4月28日,以“天人长安,创意自然一一城市与自然和谐共生”为主题的世界园艺博览会在西安隆重开园,这次园艺会的门票分为个人票和团体票两大类,其中个人票设置有三种:
某社区居委会为奖励“和谐家庭”,欲购买个人票100张,其中B种票的张数是A种票张数的3倍还多8张,设购买A种票张数为x,C种票张数为y
(1)写出y与x之间的函数关系式;
(2)设购票总费用为W元,求出W(元)与X(张)之间的函数关系式;
(3)若每种票至少购买1张,其中购买A种票不少于20张,则有几种购票方案?并求出购票总费用最少时,购买A,B,C三种票的张数.
| 票得种类 | 夜票(A) | 平日普通票(B) | 指定日普通票(C) |
| 单价(元/张) | 60 | 100 | 150 |
(1)写出y与x之间的函数关系式;
(2)设购票总费用为W元,求出W(元)与X(张)之间的函数关系式;
(3)若每种票至少购买1张,其中购买A种票不少于20张,则有几种购票方案?并求出购票总费用最少时,购买A,B,C三种票的张数.
解(1)B中票数为:3x+8
则y=100﹣x﹣3x﹣8化简得,
y=﹣4x+92
即y与x之间的函数关系式为:y=﹣4x+92
(2)w=60x+100(3x+8)+150(﹣4x+92)化简得,
w=﹣240x+14600
即购票总费用W与X(张)之间的函数关系式为:w=﹣240x+14600
(3)由题意得,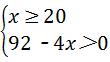 解得,
解得,
20≤x<23
∵x是正整数,∴x可取20、21、22
那么共有3种购票方案.
从函数关系式w=﹣240x+14600可以看出w随x的增大而减小,
当x=22时,w的最值最小,即当A票购买22张时,购票的总费用最少.
购票总费用最少时,购买A、B、C三种票的张数分别为22、74、4.
则y=100﹣x﹣3x﹣8化简得,
y=﹣4x+92
即y与x之间的函数关系式为:y=﹣4x+92
(2)w=60x+100(3x+8)+150(﹣4x+92)化简得,
w=﹣240x+14600
即购票总费用W与X(张)之间的函数关系式为:w=﹣240x+14600
(3)由题意得,
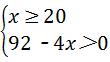 解得,
解得,20≤x<23
∵x是正整数,∴x可取20、21、22
那么共有3种购票方案.
从函数关系式w=﹣240x+14600可以看出w随x的增大而减小,
当x=22时,w的最值最小,即当A票购买22张时,购票的总费用最少.
购票总费用最少时,购买A、B、C三种票的张数分别为22、74、4.
略

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上
矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上
 ,OA=1,OC=2,
,OA=1,OC=2, 点D在边OC上且
点D在边OC上且 .
. y轴上
y轴上 是否存在点P,直线PD与矩形对角线AC交于点M,使得
是否存在点P,直线PD与矩形对角线AC交于点M,使得 为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由. 抛物线
抛物线 经过怎样平移,才能使得平移后的抛物线过点D和点E(点E在y轴正半轴上),且
经过怎样平移,才能使得平移后的抛物线过点D和点E(点E在y轴正半轴上),且 沿DE折叠后点O落在边AB上
沿DE折叠后点O落在边AB上 处?
处?
 交于y轴与点E,交AB于点F
交于y轴与点E,交AB于点F
 时,求证:∠BEF=∠BAO
时,求证:∠BEF=∠BAO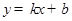 的图象经过A(-3,0)和B(O,2)两点,则
的图象经过A(-3,0)和B(O,2)两点,则 >0的解集是 .
>0的解集是 .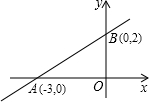
 ,高为
,高为 .如果将底边增加1,高减少1,为了使面积不变,则
.如果将底边增加1,高减少1,为了使面积不变,则