��Ŀ����
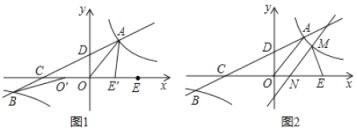
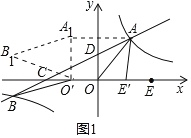
����Ŀ����ͼ1����ƽ��ֱ������ϵ![]() �У�˫����
�У�˫����![]()
![]() ��ֱ��
��ֱ��![]()
![]() ����
����![]() ��
��![]() ���㣬ֱ��
���㣬ֱ��![]() �ֱ�
�ֱ�![]() �ᡢ
�ᡢ![]() ����
����![]() ��
��![]() ���㣬
���㣬![]() Ϊ
Ϊ![]() ����һ�㣮��֪
����һ�㣮��֪![]() ��
��![]() ������Ϊ
������Ϊ![]() ��
��
 ����
����
��1�����߶�![]() ��
��![]() ��ƽ�Ƶ��߶�
��ƽ�Ƶ��߶�![]() ����ͼ1�������ƶ������У��Ƿ����ij��λ��ʹ
����ͼ1�������ƶ������У��Ƿ����ij��λ��ʹ![]() ��ֵ��������ڣ����
��ֵ��������ڣ����![]() �����ֵ����ʱ��
�����ֵ����ʱ��![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
��2����ֱ��![]() ������
������![]() ƽ�ƣ�ƽ�ƹ����н�
ƽ�ƣ�ƽ�ƹ����н�![]()
![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() ��
��![]() ����
����![]() �غϣ�����
�غϣ�����![]() ���ڵ�
���ڵ�![]() ����ͼ��������ƽ�ƹ����У��Ƿ����ij��λ��ʹ
����ͼ��������ƽ�ƹ����У��Ƿ����ij��λ��ʹ![]() Ϊ��
Ϊ��![]() Ϊ���ĵ��������Σ������ڣ����
Ϊ���ĵ��������Σ������ڣ����![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��|BO�䩁AE��|�����ֵΪ![]() ����ʱ��O������꣨��
����ʱ��O������꣨��![]() ��0����
��0����
��2�����ڣ���M������Ϊ��![]() ��
��![]() ����8��
����8��![]() ��
��
��������
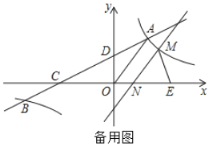
��1����A����ƽ��5����λ��A1����2��4������B����x��ĶԳƵ�B1������|BO�䩁AE��|��|BO�䩁A1O��|��B1O�䩁A1O��|��A1B1����취���A1B1��ֱ��A1B1�Ľ���ʽ���ɽ�����⣮
��2����M��m��![]() ������N��m��
������N��m��![]() ��0����NE2����5��m+
��0����NE2����5��m+![]() ��2��ME2����5��m��2+��
��2��ME2����5��m��2+��![]() ��2��MN2����
��2��MN2����![]() ��2+��
��2+��![]() ��2����MN��EM��MN��NE�������Σ��ֱ����̼��ɽ�����⣮
��2����MN��EM��MN��NE�������Σ��ֱ����̼��ɽ�����⣮
�⣺��1����ͼ1�У�
��A��3��4����
��OA��![]() ��5��
��5��
��OA��OC��OE��
��OA��OC��OE��5��
��C����5��0����E��5��0����
��A��C�����������y��ax+b�õ�![]() ��
��
���![]() ��
��
��ֱ�ߵĽ���ʽΪ![]() ��
��
��A��3��4������y��![]() �У��õ�k��12��
�У��õ�k��12��
�෴���������Ľ���ʽΪy��![]() ��
��
��A����ƽ��5����λ��A1����2��4������B����x��ĶԳƵ�B1��
����|BO�䩁AE��|��|BO�䩁A1O��|��B1O�䩁A1O��|��A1B1��
��ֱ��AC��![]() ��
��
˫���ߣ�y��![]()
��![]() ��
��![]()
��![]() ��
��
ֱ��A1B1��![]() ��
��
��y��0���ɵ�![]() ��
��
��O�䣨��![]() ��0����
��0����
��|BO�䩁AE��|�����ֵΪ![]() ����ʱ��O������꣨��
����ʱ��O������꣨��![]() ��0����
��0����
��2����M��m��![]() ������N��m��
������N��m��![]() ��0����NE2����5��m+
��0����NE2����5��m+![]() ��2��ME2����5��m��2+��
��2��ME2����5��m��2+��![]() ��2��MN2����
��2��MN2����![]() ��2+��
��2+��![]() ��2
��2
��MN��ME��������5��m��2+��![]() ��2����
��2����![]() ��2+��
��2+��![]()
![]() ��
��![]() ����������
����������
��M��![]() ��
��![]() ����
����
��MN��NE������5��m+![]() ��2����
��2����![]() ��2+��
��2+��![]() ��2�����m��8��3����������
��2�����m��8��3����������
��M��8��![]() ����
����
�������������������ĵ�M������Ϊ��![]() ��
��![]() ����8��
����8��![]() ����
����

 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
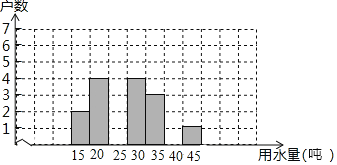
��ͨ����ͬ����ϰ��ϵ�д�����Ŀ���±���2018�����·�ij����С�������ȡ20���������ˮ�������
����ˮ��/�� | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
���� | 2 | 4 | m | 4 | 3 | 0 | 1 |
��1�����m���� �������仭����20����ͥ���·��õ���������ͳ��ͼ��
��2�����ϱ����й���Ϣ��������ҳ��±��е�ͳ�������������������У�
ͳ�������� | ���� | ��λ�� | ƽ���� |
���� | �� �� | �� �� | �� �� |
��3��Ϊ�˳�������Լ��ˮ��ɫ����������ʶ������������ˮ��˾ʵ�С��ݼ���ˮ������Ʒѡ����۸�����£�
����ˮ�ݼ��� | ��30�����ڣ� | ������30�ֵIJ��֣� |
���ۣ�Ԫ/�֣� | 2.4 | 4 |
�����С����500����ͥ�������������ݣ�������С�����·��ж��ٻ���ͥ�ڢ���
��4�����ϱ��շѣ����ij�û����½�ˮ��120Ԫ�����ʸ��û�������ˮ���ٶ֣�
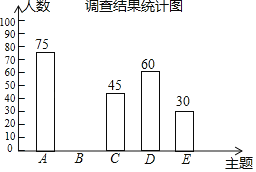
����Ŀ��2019��3��19�գ�����ʡ�����������������ƽ���Сѧ����ѧ���е�ʵʩ��������ij��ѧΪ��ʵ��������ѧ���ṩ��������������ʽ��ѧ��·��A������ɫ��������B�������غ�����C�������ʺ�������D������̬��������E�����ϼҺ�����Ϊ�˽�ѧ����ϲ����һ����ѧ��·��ÿ��ֻѡȡһ�֣��������ȡ�˲���ѧ�����е��飬�����������Ƴ����²�������ͳ�Ʊ���ͳ��ͼ������������Ϣ����������⣺
������ͳ�Ʊ�
���� | ����/�� | �ٷֱ� |
A | 75 | n% |
B | m | 30% |
C | 45 | 15% |
D | 60 | |
E | 30 |
��1�����ν��ܵ����������Ϊ�� ���ˣ�ͳ�Ʊ���m���� ����n���� ����
��2����ȫ����ͳ��ͼ��
��3����������ͳ��ͼ��Ϊ����ͳ��ͼ��������̬������������·�������ε�Բ�ĽǶ����� ����
��4������ʵ����ѧ����ѧ��3000�ˣ���ݴ˹��Ƹ�У��ϲ�����ϼҺ�����������·��ѧ���ж����ˣ�