题目内容
已知半径为5的⊙O中，弦AB=5
，弦AC=5，则∠BAC的度数是（ ）
| 2 |
| A、15° |
| B、210° |
| C、105°或15° |
| D、210°或30° |
分析：连接OC，OA，OB，根据已知可得到△OAC是等边三角形，△OAB是等腰直角三角形，从而分两种情况进行分析，不难求得∠BAC的度数．
解答：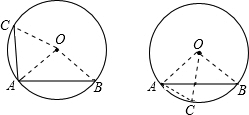
解：连接OC，OA，OB
∵OC=OA=AC=5
∴△OAC是等边三角形
∴∠CAO=60°
∵OA=OB=5，AB=5
∴OA2+OB2=50=AB2
∴△OAB是等腰直角三角形．
∴∠OAB=45°
点C的位置有两种情况：
如图，C不在弧AB上时：∠BAC=∠CAO+∠OAB=60°+45°=105°
如图，C在弧AB上时：∠BAC=∠CAO-∠OAB=60°-45°=15°．
故选C．
解：连接OC，OA，OB∵OC=OA=AC=5
∴△OAC是等边三角形
∴∠CAO=60°
∵OA=OB=5，AB=5
| 2 |
∴OA2+OB2=50=AB2
∴△OAB是等腰直角三角形．
∴∠OAB=45°
点C的位置有两种情况：
如图，C不在弧AB上时：∠BAC=∠CAO+∠OAB=60°+45°=105°
如图，C在弧AB上时：∠BAC=∠CAO-∠OAB=60°-45°=15°．
故选C．
点评：本题利用了等边三角形的判定和性质，勾股定理的逆定理求解．
练习册系列答案
名校课堂系列答案
相关题目