题目内容
（2003•台湾）如图所示，△ABC是边长为a的正三角形纸张，今在各角剪去一个三角形，使得剩下的六边形PQRSTU为正六边形，则此正六边形的周长为何（ ）
A．2a
B．3a
C．
aD．
a
【答案】分析：由六边形PQRSTU为正六边形，则六边相等，故AP=PU=UB，所以PU=
，所以六边形PQRSTU=
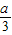×6．
解答：解：△ABC是边长为a的正三角形纸张，今在各角剪去一个三角形，使得剩下的六边形PQRSTU为正六边形，则UPQRST是各边的三等分点；故正六边形的周长比三角形的周长小了
；即其周长为2a．
故选A．
点评：本题考查等边三角形的性质与运用，其三边相等，三个内角相等，均为60度．
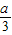，所以六边形PQRSTU=×6．解答：解：△ABC是边长为a的正三角形纸张，今在各角剪去一个三角形，使得剩下的六边形PQRSTU为正六边形，则UPQRST是各边的三等分点；故正六边形的周长比三角形的周长小了
；即其周长为2a．故选A．
点评：本题考查等边三角形的性质与运用，其三边相等，三个内角相等，均为60度．
练习册系列答案
名校课堂系列答案
相关题目
（2003•台湾）如图所示，△ABC中，∠ABC=90°，O为△ABC的外心，∠C=60°，BC=2．若△AOB面积=a，△OBC面积=b，则下列叙述何者正确（ ）
a
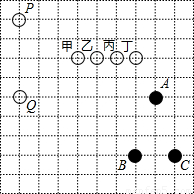
a