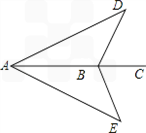
题目内容
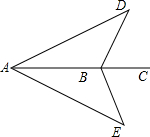 如图,一艘轮船沿AC方向航行,轮船在点A时测得航线两侧的两个灯塔与航线的夹角相等,当轮船到达点B时测得这两个灯塔与航线的夹角仍然相等,这时轮船与两个灯塔的距离是否相等?为什么?
如图,一艘轮船沿AC方向航行,轮船在点A时测得航线两侧的两个灯塔与航线的夹角相等,当轮船到达点B时测得这两个灯塔与航线的夹角仍然相等,这时轮船与两个灯塔的距离是否相等?为什么?
分析:根据轮船在点A时两个灯塔与航线的夹角相等可得∠DAB=∠EAB,轮船到达点B时两个灯塔与航线的夹角仍然相等可得∠1=∠2,再根据等角的补角相等推出∠3=∠4,然后利用角边角定理证明△ABD与△ABE全等,然后根据全等三角形对应边相等即可证明.
解答: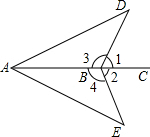 解:到达点B时轮船与两个灯塔的距离相等.
解:到达点B时轮船与两个灯塔的距离相等.
理由如下:
根据题意得,∠DAB=∠EAB,∠1=∠2,
∵∠1+∠3=180°,∠2+∠4=180°,
∴∠3=∠4,
在△ABD与△ABE,
,
∴△ABD≌△ABE(ASA),
∴BD=BE.
即,到达点B时轮船与两个灯塔的距离相等.
 解:到达点B时轮船与两个灯塔的距离相等.
解:到达点B时轮船与两个灯塔的距离相等.理由如下:
根据题意得,∠DAB=∠EAB,∠1=∠2,
∵∠1+∠3=180°,∠2+∠4=180°,
∴∠3=∠4,
在△ABD与△ABE,
|
∴△ABD≌△ABE(ASA),
∴BD=BE.
即,到达点B时轮船与两个灯塔的距离相等.
点评:本题考查了全等三角形的应用,根据等角的补角相等推出∠3=∠4是证明三角形全等的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
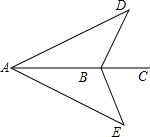 如图,一艘轮船沿AC方向航行,轮船在点A时测得航线两侧的两个灯塔与航线的夹角相等,当轮船到达点B时测得这两个灯塔与航线的夹角仍然相等,这时轮船与两个灯塔的距离是否相等?为什么?
如图,一艘轮船沿AC方向航行,轮船在点A时测得航线两侧的两个灯塔与航线的夹角相等,当轮船到达点B时测得这两个灯塔与航线的夹角仍然相等,这时轮船与两个灯塔的距离是否相等?为什么?