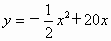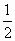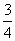题目内容
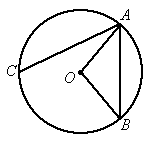
(2005 青岛)在青岛市开展的创城活动中,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成,图所示.若设花园的BC边长为x m,花园的面积为 .
.

(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)满足条件的花园面积能达到 吗?若能,求出此时x的值;若不能,请说明理由;
吗?若能,求出此时x的值;若不能,请说明理由;
(3)根据(1)中求得的函数关系式,描述其图像的变化趋势;并结合题意判断当x取何值时,花园的面积最大?最大面积为多少?
答案:略
解析:
提示:
解析:
|
解 (1)根据题意得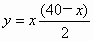 , ,
∴ 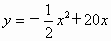 (0<x≤15). (0<x≤15).
(2) 当y=200时,即 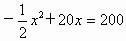 . .
∴ 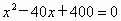 . .
解得 x=20>15.∵ 0<x≤15,∴此花园的面积不能达到 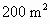 . .
(3) ∴当 0<x≤15时,y随x的增大而增大.∴当 x=15时,y有最大值,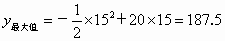 , ,
即当 x=15时,花园面积最大,最大面积为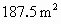 . . |
提示:
|
理解二次函数的性质及用二次函数的性质解决实际问题. |

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目