题目内容
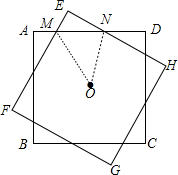 在一次研究性学习活动中,某小组将两张互相重合的正方形纸片ABCD和EFGH的中心O用图钉固定住,保持正方形ABCD不动,顺时针旋转正方形EFGH,如图所示.
在一次研究性学习活动中,某小组将两张互相重合的正方形纸片ABCD和EFGH的中心O用图钉固定住,保持正方形ABCD不动,顺时针旋转正方形EFGH,如图所示.(1)小组成员经观察、测量,发现在旋转过程中,有许多有趣的结论.下面是旋转角度小于90°时他们得到的一些猜想:
①ME=MA;
②两张正方形纸片的重叠部分的面积为定值;
③∠MON保持45°不变.
请你对这三个猜想作出判断(正确的在序号后的括号内打上“√”,错误的打上“×”):
①( );②( );③( )
(2)小组成员还发现:(1)中的△EMN的面积S随着旋转角度∠AOE的变化而变化.请你指出在怎样的位置时△EMN的面积S取得最大值.(不必证明)
(3)上面的三个猜想中若有正确的,请选择其中的一个给予证明;若都是错误的,请选择其一说明理由.
分析:根据正方形的性质和旋转的性质可知,∠OAE=∠OEA,∠MAO=∠MEO=45°,∴∠MAE=∠MEA,所以ME=MA;∠MOE+∠NOE=
∠AOD=
×90°=45°,即∠MON保持45°不变.并且当∠AOE=45°时,△EMN的面积S取得最大值.
| 1 |
| 2 |
| 1 |
| 2 |
解答: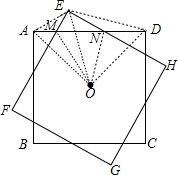 解:(1)①(√);②(×);③(√).
解:(1)①(√);②(×);③(√).
(2)当∠AOE=45°时,△EMN的面积S取得最大值.
(3)证明:对于猜想①,连接OA、OE、AE、OD、ED.由已知得OA=OE,
∴∠OAE=∠OEA.
又∵∠OAM=∠OEM=45°,
∴∠OAE-∠OAM=∠OEA-∠OEM,即∠MAE=∠MEA.
∴ME=MA.
对于猜想③,证得OM平分∠EOA,同理ON平分∠DOE,
∴∠MOE+∠NOE=
∠AOD=
×90°=45°,即∠MON保持45°不变.
 解:(1)①(√);②(×);③(√).
解:(1)①(√);②(×);③(√).(2)当∠AOE=45°时,△EMN的面积S取得最大值.
(3)证明:对于猜想①,连接OA、OE、AE、OD、ED.由已知得OA=OE,
∴∠OAE=∠OEA.
又∵∠OAM=∠OEM=45°,
∴∠OAE-∠OAM=∠OEA-∠OEM,即∠MAE=∠MEA.
∴ME=MA.
对于猜想③,证得OM平分∠EOA,同理ON平分∠DOE,
∴∠MOE+∠NOE=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查旋转的性质和正方形的性质.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.正方形是特殊条件最多的图形,它的特性要重点掌握.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
 (2011•鄞州区模拟)在一次研究性学习活动中,某小组将两张互相重合的正方形纸片ABCD和EFGH的中心O用图钉固定住,保持正方形ABCD不动,顺时针旋转正方形EFGH,如图所示.
(2011•鄞州区模拟)在一次研究性学习活动中,某小组将两张互相重合的正方形纸片ABCD和EFGH的中心O用图钉固定住,保持正方形ABCD不动,顺时针旋转正方形EFGH,如图所示. 、测量,发现在旋转过程中,有许多有趣的结论.下面是旋转角度小于90°时他们得到的一些猜想:
、测量,发现在旋转过程中,有许多有趣的结论.下面是旋转角度小于90°时他们得到的一些猜想: