题目内容
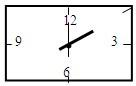某课外学习小组在设计一个长方形时钟钟面时，欲使长方形的宽为20厘米，时钟的中心在长方形对角线的交点上，数字2在长方形的顶点上，数字3、6、9、12标在所在边的中点上，如图所示．则长方形的长应为分析：根据题意即可求得∠AOC=2∠BOC，即可求得∠BOC=30°，故OB=
BC，即可求得长方形的长是宽的
倍，即可解题．
| 3 |
| 3 |
解答：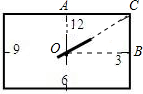
解：由题意知∠AOC=2∠BOC，
∵∠AOC+∠BOC=90°
∴∠BOC=30°，∠AOC=60°，
∴tanB=
=
，
即OB=
BC，
∴矩形ABCD长是宽的
倍，
∴长方形的长是20
厘米．
故答案为 20
．
解：由题意知∠AOC=2∠BOC，∵∠AOC+∠BOC=90°
∴∠BOC=30°，∠AOC=60°，
∴tanB=
| BC |
| OB |
| ||
| 3 |
即OB=
| 3 |
∴矩形ABCD长是宽的
| 3 |
∴长方形的长是20
| 3 |
故答案为 20
| 3 |
点评：本题考查了直角三角形中tanB的计算，考查了特殊角的正切值的计算，本题中找到∠AOC=2∠BOC是解题的关键．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
：要画出必要的、反映解题思路的辅助线）；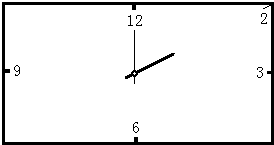
长方形对角线的交点上，数字2在长方形的顶点上，数字3、6、9、12标在所在边的中点上，如图所示．
