题目内容
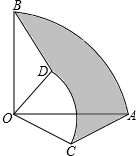 圆心角都是90°的扇形OAB与扇形OCD如图所示那样叠放在一起,连接AC、BD.
圆心角都是90°的扇形OAB与扇形OCD如图所示那样叠放在一起,连接AC、BD.(1)求证:△AOC≌△BOD;
(2)若OA=3cm,OC=1cm,求阴影部分的面积.
分析:(1)利用SAS证明全等即可;
(2)根据扇形面面积公式求出阴影部分的面积.
(2)根据扇形面面积公式求出阴影部分的面积.
解答:(1)证明:∵∠COD=∠AOB=90°,
∴∠AOC+∠AOD=∠AOD+∠BOD,
∴∠AOC=∠BOD,
又∵OA=OB,OC=OD,
∴△AOC≌△BOD;(3分)
(2)解:S阴影=S扇形AOB-S扇形COD=
π×32-
π×12=2π(cm2).
故答案为:2πcm2.
∴∠AOC+∠AOD=∠AOD+∠BOD,
∴∠AOC=∠BOD,
又∵OA=OB,OC=OD,
∴△AOC≌△BOD;(3分)
(2)解:S阴影=S扇形AOB-S扇形COD=
| 1 |
| 4 |
| 1 |
| 4 |
故答案为:2πcm2.
点评:此题考查两个知识点:全等三角形的判定和如何计算扇形的面积.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
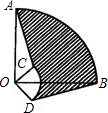 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,OC=1,分别连接AC、BD,则图中阴影部分的面积为( )
如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,OC=1,分别连接AC、BD,则图中阴影部分的面积为( )A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
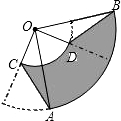
 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC,BD.
如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC,BD.