题目内容
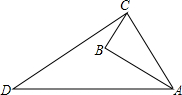 如图是一个机器零件示意图,∠ACD=90°是衡量这个零件是否合格的一项指标.现测得AB=4cm,BC=3cm,AD=13cm,CD=12cm,∠ABC=90°,根据这些条件,能否知道∠ACD是否等90°?
如图是一个机器零件示意图,∠ACD=90°是衡量这个零件是否合格的一项指标.现测得AB=4cm,BC=3cm,AD=13cm,CD=12cm,∠ABC=90°,根据这些条件,能否知道∠ACD是否等90°?分析:根据AB=4cm,BC=3cm,∠ABC=90°,根据勾股定理可求AC的长,再根据勾股定理的逆定理,即可知道∠ACD是否等90°.
解答:解:∵在Rt△ABC中,AB=4cm,BC=3cm,∠ABC=90°,
∴AC=
=5cm,
在△ACD中,∵AD=13cm,CD=12cm,AC=5cm,
∴AD2=169,CD2+AC2=169,
∴AD2=CD2+AC2,
∴∠ACD=90°.
∴AC=
| 42+32 |
在△ACD中,∵AD=13cm,CD=12cm,AC=5cm,
∴AD2=169,CD2+AC2=169,
∴AD2=CD2+AC2,
∴∠ACD=90°.
点评:考查了勾股定理和勾股定理的逆定理,勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
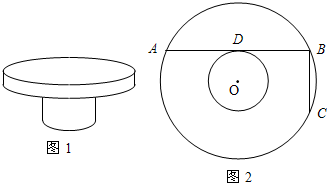


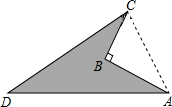 如图阴影部分所示,是一个机器零件的平面示意图,现测得AB=4cm,BC=3cm,AC=5cm,CD=12cm,∠ABC=90°,AD=13.求这个机器零件的面积S.
如图阴影部分所示,是一个机器零件的平面示意图,现测得AB=4cm,BC=3cm,AC=5cm,CD=12cm,∠ABC=90°,AD=13.求这个机器零件的面积S.