题目内容
等边△ABC的周长为6,则等边△ABC的面积是________.

分析:根据等边三角形三线合一的性质,可求得D为BC中点且AD⊥BC,根据勾股定理即可求AD的值,根据AD、BC即可计算△ABC的面积.
解答:周长为6,则等边△ABC的边长为2,
∵AD为BC边上的高,则D为BC的中点,
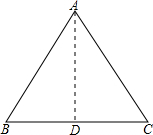
∴BD=DC=1,∴AD=
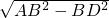 =
= ,
,∴等边△ABC的面积=
 BC•AD=
BC•AD= ×2×
×2× =
= ,
,故答案为
 .
.点评:本题考查了等边三角形三线合一的性质,考查了勾股定理在直角三角形中的运用,考查了三角形面积的计算,本题中根据勾股定理计算AD的长是解题的关键.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
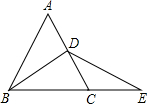 如图,已知等边△ABC的周长为6,BD是AC边的中线,E为BC延长线上一点,CD=CE,那么△BDE的周长是( )
如图,已知等边△ABC的周长为6,BD是AC边的中线,E为BC延长线上一点,CD=CE,那么△BDE的周长是( )A、5+2
| ||
B、5+
| ||
C、3+2
| ||
D、3+
|
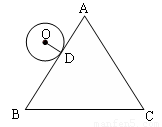
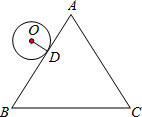 (2012•北海)如图,等边△ABC的周长为6π,半径是1的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了( )
(2012•北海)如图,等边△ABC的周长为6π,半径是1的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了( ) 已知等边△ABC的周长为6厘米,求它的面积.
已知等边△ABC的周长为6厘米,求它的面积.