题目内容
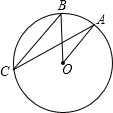如图，A，B，C是圆O上三点， |
| AB |
| A、15° | B、25° |
| C、30° | D、40° |
分析：由
的度数是50°，得到∠AOB=50°，再利用圆周角定理求出∠BCA，然后由三角形的内角和得到∠OAC．
|
| AB |
解答：解：∵
的度数是50°，
∴∠AOB=50°，
∴∠BCA=25°，
又∵∠OAC+∠BOA=∠BCA+∠CBO，即∠OAC+50°=25°+40°，
∴∠OAC=15°．
故选A．
|
| AB |
∴∠AOB=50°，
∴∠BCA=25°，
又∵∠OAC+∠BOA=∠BCA+∠CBO，即∠OAC+50°=25°+40°，
∴∠OAC=15°．
故选A．
点评：本题考查了圆周角定理．在同圆或等圆中，同弧和等弧所对的圆周角相等，一条弧所对的圆周角是它所对的圆心角的一半．同时考查了圆心角的度数等于它所对的弧的度数．
练习册系列答案
相关题目
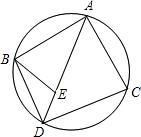如图，AB，AC，AD是圆中的三条弦，点E在AD上，且AB=AC=AE．请你说明以下各式成立的理由：
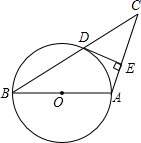如图所示，已知AB是圆O的直径，圆O过BC的中点D，且DE⊥AC．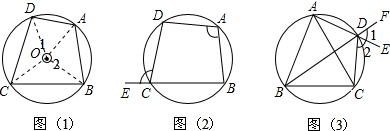
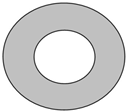如图，某一零件的表面是圆环形，圆环表面上涂刷油漆，已知圆环的内圆半径是3.6dm，外圆半径是5.6dm，每平方分米的面积需要油漆a克，用a来表示这个零件所需要的油漆的重量．（π取3.14）