题目内容
等腰三角形中,两腰和底的长分别是10和13,求三角形的三个内角的度数(精确到l′).
如右图所示,AB=AC=10,BC=13,AD是底边上的高,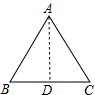
∵AD是底边上的高,
∴AD⊥BC,
又∵AB=AC,
∴BD=CD=6.5,∠BAD=∠CAD=
∠BAC,
在Rt△ABD中,sin∠BAD=
=
=0.65,
∴∠BAD≈40°32′,
∴∠BAC≈2∠BAD≈81°4′,∠B=∠C≈49°28′.
故△ABC的三个内角分别为:81°4′,49°28′,49°28′.

∵AD是底边上的高,
∴AD⊥BC,
又∵AB=AC,
∴BD=CD=6.5,∠BAD=∠CAD=
| 1 |
| 2 |
在Rt△ABD中,sin∠BAD=
| BD |
| AB |
| 6.5 |
| 10 |
∴∠BAD≈40°32′,
∴∠BAC≈2∠BAD≈81°4′,∠B=∠C≈49°28′.
故△ABC的三个内角分别为:81°4′,49°28′,49°28′.

练习册系列答案
相关题目