题目内容
Rt△ABC的斜边AB=5,直角边AC=3,若AB与⊙C相切,则⊙C的半径是
2.4
2.4
.分析:根据题意画出相应的图形,如图所示,当圆C与AB相切于点D时,连接CD,根据切线的性质得到CD垂直于AB,此时CD即为圆C的半径,在直角三角形ACB中,由AB及AC的长,利用勾股定理求出BC的长,再由三角形ABC的面积等于两直角边乘积的一半来求,也可以由斜边AB乘以斜边上的高CD来求,根据面积相等可得出斜边上高CD的长,即为此时圆C的半径.
解答:解:根据题意画出图形,如图所示:
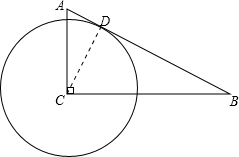
∵Rt△ABC的斜边AB=5,直角边AC=3,
∴根据勾股定理得:BC=
=4,
∵圆C与AB相切于点D,连接CD,
∴CD⊥AB,
又∵S△ABC=
AB•CD=
AC•BC,
∴CD=
=
=2.4,
则AB与圆C相切时,圆C的半径为2.4.
故答案为:2.4.

∵Rt△ABC的斜边AB=5,直角边AC=3,
∴根据勾股定理得:BC=
| AB2-AC2 |
∵圆C与AB相切于点D,连接CD,
∴CD⊥AB,
又∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=
| AC•BC |
| AB |
| 3×4 |
| 5 |
则AB与圆C相切时,圆C的半径为2.4.
故答案为:2.4.
点评:此题考查了切线的性质,勾股定理,以及三角形的面积求法,利用了数形结合的思想,其中圆的切线垂直于过切点的直径,且此时圆心到切线的距离等于圆的半径,熟练掌握这些性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
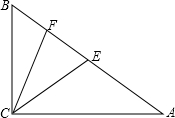 如图,E、F分别是Rt△ABC的斜边AB上的两点,AF=AC,BE=BC,则∠ECF=
如图,E、F分别是Rt△ABC的斜边AB上的两点,AF=AC,BE=BC,则∠ECF=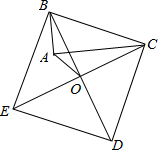 如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连接AO,如果AB=3,AO=
如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连接AO,如果AB=3,AO=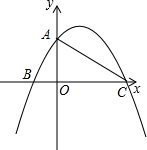 (2013•封开县一模)已知,如图,在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,直角顶点A在y轴的正半轴上,A(0,2),B(-1,0).
(2013•封开县一模)已知,如图,在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,直角顶点A在y轴的正半轴上,A(0,2),B(-1,0).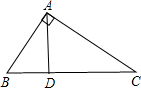 如图,AD是Rt△ABC的斜边BC上的高线,要使△ACD的面积是△ABC和△ABD面积的比例中项,请你添加一个适当的条件:
如图,AD是Rt△ABC的斜边BC上的高线,要使△ACD的面积是△ABC和△ABD面积的比例中项,请你添加一个适当的条件: