题目内容
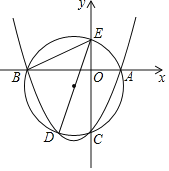
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,AC与⊙O交于D,OE∥BD交⊙O于E.
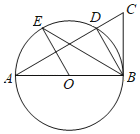
(1)求证:BE平分∠ABD.
(2)当∠A=∠E,BC=2时,求⊙O的面积.
【答案】(1)见解析;(2)⊙O的面积为3π.
【解析】
(1)根据等腰三角形的性质得到∠E=∠ABE,根据平行线的性质得到∠E=∠EBD,等量代换得到∠OBE=∠EBD,于是得到结论;
(2)根据圆周角定理得到∠ADB=90°,得到∠A=30°,根据切线的性质得到∠ABC=90°,解直角三角形即可得到结论.
(1)证明:∵OE=OB,
∴∠E=∠ABE,
∵OE∥BD,
∴∠E=∠EBD,
∴∠OBE=∠EBD,
∴BE平分∠ABD;
(2)解:∵∠A=∠E,
∴∠ABD=2∠A,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠A=30°,
∵BC是⊙O的切线,
∴∠ABC=90°,
∵BC=2,
∴AB=![]() BC=2
BC=2![]() ,
,
∴AO=![]() ,
,
∴⊙O的面积=3π.

练习册系列答案
相关题目