题目内容
如图,原点O是△ABC和△A′B′C′的位似中心,点A(1,0)与点A′(-2,0)是对应点,点B(2,2),则B′点的坐标________.

(-4,-4)
分析:根据题意,由A与A′的坐标,可得△ABC和△A′B′C′的位似比,又由位似的性质可得E所在的象限,计算可得答案.
解答:根据题意,原点O是△ABC和△A′B′C′的位似中心,
必有 =
= ;
;
又有点A(1,0)与点A′(-2,0);
可得 =2,
=2,
结合图象,B′在第三象限,
故B′点的坐标是(-4,-4).
点评:本题考查了位似的性质的运用,要借助位似中心及位似比来解题.
分析:根据题意,由A与A′的坐标,可得△ABC和△A′B′C′的位似比,又由位似的性质可得E所在的象限,计算可得答案.
解答:根据题意,原点O是△ABC和△A′B′C′的位似中心,
必有
 =
= ;
;又有点A(1,0)与点A′(-2,0);
可得
 =2,
=2,结合图象,B′在第三象限,
故B′点的坐标是(-4,-4).
点评:本题考查了位似的性质的运用,要借助位似中心及位似比来解题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
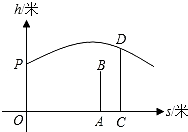 m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是
m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是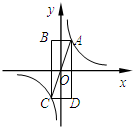 如图,原点O是矩形ABCD的对称中心,顶点A、C在反比例函数图象上,AB平行x轴.若矩形ABCD的面积为8,那么反比例函数的解析式是
如图,原点O是矩形ABCD的对称中心,顶点A、C在反比例函数图象上,AB平行x轴.若矩形ABCD的面积为8,那么反比例函数的解析式是 如图,原点O是矩形ABCD的对称中心,顶点A、C在反比例函数图象上,AB平行x轴.若矩形ABCD的面积为8,那么反比例函数的解析式是________.
如图,原点O是矩形ABCD的对称中心,顶点A、C在反比例函数图象上,AB平行x轴.若矩形ABCD的面积为8,那么反比例函数的解析式是________.
