题目内容
图1是由五个边长都是1的正方形纸片拼接而成的,过点A1的直线分别与BC1、BE交于点M、N,且图1被直线MN分成面积相等的上、下两部分.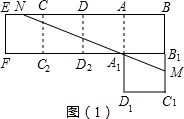
(1)求
| 1 |
| MB |
| 1 |
| NB |
(2)求MB、NB的长;
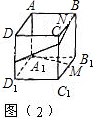
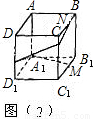
(3)将图1沿虚线折成一个无盖的正方体纸盒(图2)后,求点M、N间的距离.
分析:(1)本题可通过相似三角形A1B1M和NBM得出的关于NB,A1B1,MB,MB1的比例关系式来求,比例关系式中A1B1,BB1均为正方形的边长,长度都是1,因此可将它们的值代入比例关系式中,将所得的式子经过变形即可得出所求的值;
(2)由于直线MN将图(1)的图形分成面积相等的两部分,因此△BMN的面积为
,由此可求出MB•NB的值,根据(1)已经得出的MB+NB=MB•NB可求出MB+NB的值,由此可根据韦达定理列出以MB,NB为根的一元二次方程,经过解方程即可求出MB、NB的值;
(3)根据(2)的结果,不难得出B1M=EN,由于折叠后E与B点重合,因此B1M=BN,那么四边形B1MNB是个矩形,因此MN的长为正方形的边长.
(2)由于直线MN将图(1)的图形分成面积相等的两部分,因此△BMN的面积为
| 5 |
| 2 |
(3)根据(2)的结果,不难得出B1M=EN,由于折叠后E与B点重合,因此B1M=BN,那么四边形B1MNB是个矩形,因此MN的长为正方形的边长.
解答:解:(1)∵△A1B1M∽△NBM且A1B1=BB1=1,
∴
=
,
即
=
整理,得MB+NB=MB•NB,
两边同除以MB•NB得
+
=1;
(2)由题意得
MB•NB=
,
即MB•NB=5,
又由(1)可知MB+NB=MB•NB=5,
∴MB、NB分别是方程x2-5x+5=0的两个实数根.
解方程,得x1=
,x2=
;
∵MB<NB,
∴MB=
,NB=
;
(3)由(2)知B1M=
-1=
,
EN=4-
=
,
∵图(2)中的BN与图(1)中的EN相等,
∴BN=B1M;
∴四边形BB1MN是矩形,
∴MN的长是1.
∴
| NB |
| A1B1 |
| MB |
| MB1 |
即
| NB |
| 1 |
| MB |
| MB-1 |
整理,得MB+NB=MB•NB,
两边同除以MB•NB得
| 1 |
| MB |
| 1 |
| NB |
(2)由题意得
| 1 |
| 2 |
| 5 |
| 2 |
即MB•NB=5,
又由(1)可知MB+NB=MB•NB=5,
∴MB、NB分别是方程x2-5x+5=0的两个实数根.
解方程,得x1=
5+
| ||
| 2 |
5-
| ||
| 2 |
∵MB<NB,
∴MB=
5-
| ||
| 2 |
5+
| ||
| 2 |
(3)由(2)知B1M=
5-
| ||
| 2 |
3-
| ||
| 2 |
EN=4-
5+
| ||
| 2 |
3-
| ||
| 2 |
∵图(2)中的BN与图(1)中的EN相等,
∴BN=B1M;
∴四边形BB1MN是矩形,
∴MN的长是1.
点评:本题主要考查了相似三角形的判定和性质,正方形的性质,一元二次方程的应用等知识点,综合性比较强.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
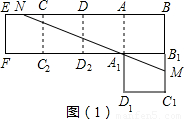

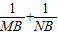 的值;
的值;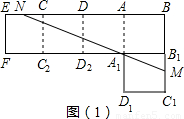

 的值;
的值;
 的值;
的值;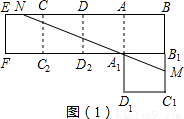

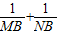 的值;
的值;