题目内容
将图(1)中的矩形ABCD沿对角线AC剪开,再把△ABC沿着AD方向平移,得到图(2)中的△A′BC′,AB=6,BC=8.(1)除△ADC与△C′BA′全等外,你还可以指出哪几对全等的三角形(不能添加辅助线和字母)?
(2)试证明四边形A′ECF是平行四边形;
(3)当图(2)中的BC多长时,平行四边形A′ECF的面积最大?

分析:(1)利用平移的性质得出对应线段相等,再利用全等三角形的判定求出即可;
(2)利用平行四边形的性质,首先得出△A′DF≌△CBE,再利用A′E=CF,得出四边形是平行四边形;
(3)利用相似三角形的性质得出DF=
x,进而得出平行四边形的面积,利用二次函数的增减性求出即可.
(2)利用平行四边形的性质,首先得出△A′DF≌△CBE,再利用A′E=CF,得出四边形是平行四边形;
(3)利用相似三角形的性质得出DF=
| 3 |
| 4 |
解答:(1)解:由平移的性质可知:
∵AA′=CC′,
又∵∠A=∠C′,
∠AA′E=∠C′CF=90°,
∴△AA′E≌△C′CF.
∵A′C′∥AC,
∴∠DCE=∠DFA′,
∵∠BCE+∠ECF=90°,∠A′FD+∠DA′F=90°
∴∠ECB=∠DA′F,
∵BC=A′D,∠B=∠D,
∴△A′DF≌△CBE,
有两对全等三角形,分别为:△AA′E≌△C′CF,△A′DF≌△CBE;
(2)证明:由平移的性质可知:A′E∥CF,A′F∥CE,
∴四边形A′ECF是平行四边形.
∴A′F=CE,A′E=CF.
∵A′B=CD,
∴DF=BE,
又∵∠B=∠D=90°,
∴△A′DF≌△CBE.
∴A′F=CE,DF=BE,
∵A′B=DC,
∴A′B-EB=DC-DF,即A′E=CF,
∴四边形A′ECF是平行四边形;

(3)解:假设BC=x,
∴CC′=8-x,
∵AD∥BC′,
∴△DFA′∽△CFC′,
∴
=
,
∴
=
,
解得:DF=
x,
∴平行四边形A′ECF的面积为:CF×BC=
x2,
∴当x=8时,平行四边形A′ECF的面积最大.
∵AA′=CC′,
又∵∠A=∠C′,
∠AA′E=∠C′CF=90°,
∴△AA′E≌△C′CF.
∵A′C′∥AC,
∴∠DCE=∠DFA′,
∵∠BCE+∠ECF=90°,∠A′FD+∠DA′F=90°
∴∠ECB=∠DA′F,
∵BC=A′D,∠B=∠D,
∴△A′DF≌△CBE,
有两对全等三角形,分别为:△AA′E≌△C′CF,△A′DF≌△CBE;
(2)证明:由平移的性质可知:A′E∥CF,A′F∥CE,
∴四边形A′ECF是平行四边形.
∴A′F=CE,A′E=CF.
∵A′B=CD,
∴DF=BE,
又∵∠B=∠D=90°,
∴△A′DF≌△CBE.
∴A′F=CE,DF=BE,
∵A′B=DC,
∴A′B-EB=DC-DF,即A′E=CF,
∴四边形A′ECF是平行四边形;

(3)解:假设BC=x,
∴CC′=8-x,
∵AD∥BC′,
∴△DFA′∽△CFC′,
∴
| A′D |
| CC′ |
| DF |
| CF |
∴
| x |
| 8-x |
| DF |
| 6-DF |
解得:DF=
| 3 |
| 4 |
∴平行四边形A′ECF的面积为:CF×BC=
| 3 |
| 4 |
∴当x=8时,平行四边形A′ECF的面积最大.
点评:此题主要考查了相似三角形的判定与性质以及平行四边形的判定与性质和二次函数的增减性,求最值问题一般是二次函数的最值问题,应有意识的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
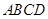 沿对角线
沿对角线 剪开,再把
剪开,再把 沿着
沿着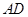 方向平移,得到图(2)中的
方向平移,得到图(2)中的 .其中
.其中 是
是 与
与 是
是 与
与 的交点.在图(2)中除
的交点.在图(2)中除 与
与 全等外,还有几对全等三角形(不得添加辅助线和字母)?请一一指出,并选择其中一对证明.
全等外,还有几对全等三角形(不得添加辅助线和字母)?请一一指出,并选择其中一对证明.
 沿对角线
沿对角线 剪开,再把
剪开,再把 沿着
沿着 方向平移,得到图(2)中的
方向平移,得到图(2)中的 .其中
.其中 是
是 与
与 是
是 与
与 的交点.在图(2)中除
的交点.在图(2)中除 与
与 全等外,还有几对全等三角形(不得添加辅助线和字母)?请一一指出,并选择其中一对证明.
全等外,还有几对全等三角形(不得添加辅助线和字母)?请一一指出,并选择其中一对证明.

