题目内容
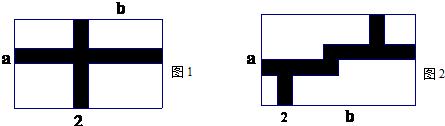
如图,一块矩形空地的一组邻边分别为a,b(单位:米),现准备在空地上修一条宽为2米的人行道(图1、2中阴影部分),人行道都与边平行或垂直;其余部分种植草坪.
(1)如图1,试用含a,b代数式表示出草坪的面积;
(2)如图2,若矩形空地的周长为72,矩形空地的面积为320,求出草坪的面积.
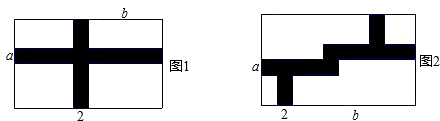
解:(1)草坪的面积为(a-2)(b-2);
(2)设矩形的长为xcm,则矩形的宽为(36-x)cm.
x(36-x)=320
解得x1=20,x2=16,
当x=20时,36-x=16;
当x=16时,36-x=20.
∴矩形的长为20m,宽为16m.
∴草坪的面积=(20-2)×(16-2)=252m2.
分析:(1)把人行道进行平移可得草坪的面积为边长为(a-2),(b-2)的长方形的面积;
(2)先设矩形的长为未知数,用周长表示矩形的宽,根据面积列出方程求正数解求得矩形的长和宽,代入(1)得到式子计算即可.
点评:考查列代数式及代数式的求法,一元二次方程的应用;把人行道平移得到草坪的形状及边长是解决本题的关键.
(2)设矩形的长为xcm,则矩形的宽为(36-x)cm.
x(36-x)=320
解得x1=20,x2=16,
当x=20时,36-x=16;
当x=16时,36-x=20.
∴矩形的长为20m,宽为16m.
∴草坪的面积=(20-2)×(16-2)=252m2.
分析:(1)把人行道进行平移可得草坪的面积为边长为(a-2),(b-2)的长方形的面积;
(2)先设矩形的长为未知数,用周长表示矩形的宽,根据面积列出方程求正数解求得矩形的长和宽,代入(1)得到式子计算即可.
点评:考查列代数式及代数式的求法,一元二次方程的应用;把人行道平移得到草坪的形状及边长是解决本题的关键.

练习册系列答案
相关题目