题目内容
用边长相等的两种正多边形进行密铺,其中一种是正八边形,则另一种正多边形可以是
- A.正三角形
- B.正方形
- C.正五边形
- D.正六边形
B
分析:正八边形的每个内角为:180°-360°÷8=135°,分别计算出正三角形,正方形,正五边形,正六边形的每个内角的度数.利用“围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角”作为相等关系列出多边形个数之间的数量关系,利用多边形的个数都是正整数可推断出能和正八边形一起密铺的多边形是正四边形.
解答:正八边形的每个内角为180°-360°÷8=135°,
A、正三角形的每个内角60°,得135m+60n=360°,n=6- m,显然m取任何正整数时,n不能得正整数,故不能铺满;
m,显然m取任何正整数时,n不能得正整数,故不能铺满;
B、正四边形的每个内角是90°,得90°+2×135°=360°,所以能铺满;
C、正五边形每个内角是180°-360°÷5=108°,得108m+135n=360°,m取任何正整数时,n不能得正整数,故不能铺满;
D、正六边形的每个内角是120度,得135m+120n=360°,n=3-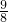 m,显然m取任何正整数时,n不能得正整数,故不能铺满.
m,显然m取任何正整数时,n不能得正整数,故不能铺满.
故选B.
点评:几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.需注意正多边形内角度数=180°-360°÷边数.
分析:正八边形的每个内角为:180°-360°÷8=135°,分别计算出正三角形,正方形,正五边形,正六边形的每个内角的度数.利用“围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角”作为相等关系列出多边形个数之间的数量关系,利用多边形的个数都是正整数可推断出能和正八边形一起密铺的多边形是正四边形.
解答:正八边形的每个内角为180°-360°÷8=135°,
A、正三角形的每个内角60°,得135m+60n=360°,n=6-
 m,显然m取任何正整数时,n不能得正整数,故不能铺满;
m,显然m取任何正整数时,n不能得正整数,故不能铺满;B、正四边形的每个内角是90°,得90°+2×135°=360°,所以能铺满;
C、正五边形每个内角是180°-360°÷5=108°,得108m+135n=360°,m取任何正整数时,n不能得正整数,故不能铺满;
D、正六边形的每个内角是120度,得135m+120n=360°,n=3-
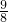 m,显然m取任何正整数时,n不能得正整数,故不能铺满.
m,显然m取任何正整数时,n不能得正整数,故不能铺满.故选B.
点评:几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.需注意正多边形内角度数=180°-360°÷边数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
用边长相等的两种正多边形进行密铺,其中一种是正八边形,则另一种正多边形可以是( )
| A、正三角形 | B、正方形 | C、正五边形 | D、正六边形 |