题目内容
【题目】如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.

(1)求作此残片所在的圆(不写作法,保留作图痕迹)
(2)求残片所在圆的面积
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心OA长为半径作圆即可;(2)连接OA,设OA=x,然后利用勾股定理列方程,解方程可得圆的半径,然后根据圆的面积公式计算即可.
试题解析:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,
以O为圆心OA长为半径作圆O就是此残片所在的圆,如图.(4分)
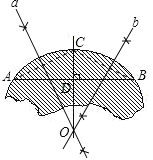
(2)连接OA,

设OA=x,AD=12cm,OD=(x-8)cm,
则根据勾股定理列方程:
x2="12"2+(x-8)2,
解得:x=13.
所以圆的面积![]() .
.

练习册系列答案
相关题目
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品每天的利润为y元。
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?最大利润是多少?
(3)该商品在销售过程中,共有多少天每天的销售利润不低于4800元?请直接写出结果。
