题目内容
已知深圳湾大酒店的三人间和双人间客房标价为:三人间为每人每天200元,双人间为每人每天300元.为吸引客源,促进旅游,在十一黄金周期间深圳湾大酒店进行优惠大酬宾,凡团 体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间,双人间客房.
体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间,双人间客房.(1)如果每个客房正好住满,并且一天一共花去住宿费6300元.求租住了三人间、双人间客房各多少间?
(2)设三人间共住了x人,一天一共花去住宿费y元,请写出y与x的函数关系式;并请在直角坐标系内画出这个函数图象;
(3)一天6300元的住宿费是否为最低?如果不是,请设计一种入住的房间正好被住满的入住方案,使住宿费用最低,并求出最低的费用.
分析:(1)设三人间有a间,双人间有b间.根据①客房人数=50;②住宿费6300 列方程组求解;
(2)根据题意,三人间住了x人,则双人间住了(50-x)人.
住宿费=100×三人间的人数+150×双人间的人数;
(3)根据x的取值范围及实际情况,运用函数的性质解答.
(2)根据题意,三人间住了x人,则双人间住了(50-x)人.
住宿费=100×三人间的人数+150×双人间的人数;
(3)根据x的取值范围及实际情况,运用函数的性质解答.
解答: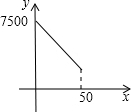 解:(1)设三人间有a间,双人间有b间.根据题意得
解:(1)设三人间有a间,双人间有b间.根据题意得
.
解得
.
答:租住了三人间8间,双人间13间.
(2)根据题意得y=100x+150(50-x)=-50x+7500,(0≤x≤50,取整数点).
(3)因为-50<0,所以y随x的增大而减小.
故当x取满足
、
为整数值的增大值时,即x=48时,住宿费用最低.
此时y=-50×48+7500=5100<6300.
答:一天6300元的住宿费不是最低;若48人入住三人间,则费用最低,为5100元.
 解:(1)设三人间有a间,双人间有b间.根据题意得
解:(1)设三人间有a间,双人间有b间.根据题意得
|
解得
|
答:租住了三人间8间,双人间13间.
(2)根据题意得y=100x+150(50-x)=-50x+7500,(0≤x≤50,取整数点).
(3)因为-50<0,所以y随x的增大而减小.
故当x取满足
| x |
| 3 |
| 50-x |
| 2 |
此时y=-50×48+7500=5100<6300.
答:一天6300元的住宿费不是最低;若48人入住三人间,则费用最低,为5100元.
点评:此题考查一次函数的应用及列方程(组)解应用题,综合性强,难度较大.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间,双人间客房.
体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间,双人间客房.