Question

如图，在锐角∠AOB的内部有一点P，点P关于OA、OB的对称点分别为E、F，
（1）△EOF一定是______三角形；
（2）若∠AOB=45°，则△EOF是______三角形．

Answer 1

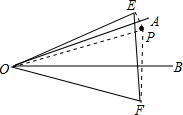
连接OP，根据轴对称的性质可得：
（1）OP=OE=OF，故△EOF一定是等腰三角形；
（2）∠AOE=∠AOP，∠BOF=∠BOP；
∴∠EOF=2（∠AOP+∠BOP）=2∠AOB；
当∠AOB=45°时，∠EOF=90°；故此时△EOF是等腰直角三角形．
故填等腰，等腰直角．