题目内容
已知:抛物线经过坐标原点.
(1)求抛物线的解析式和顶点B的坐标;
(2)设点A是抛物线与轴的另一个交点,试在
轴上确定一点P,使PA+PB最短,并求出点P的坐标;
(3)过点A作AC∥BP交轴于点C,求到直线AP、AC、CP距离相等的点的坐标.
解:(1)∵抛物线经过坐标原点,
∴ =0. 解得
.
∵ ,∴
∴
…1分
∴ . ………………………….2分
(2)令,得
=0,
解得 . ∴
………..3分
∴点A关于轴的对称点
的坐标为
.
联结,直线
与
轴的交点即为所求点P.
可求得直线的解析式:
. ∴
……………………………4分
(3)到直线AP、AC、CP距离相等的点有四个.
如图,由勾股定理得,所以△PAC为等边三角形.
易证轴所在直线平分∠PAC,BP是△PAC的一个外角的平分线.作∠PCA的平分线,交
轴于
点,交过A点的平行线于y轴的直线于
点,作△PAC的∠PCA相邻外角的平分线,交
于
点,反向延长C
交
轴于
点.可得点
就是到直线AP、AC、CP距离相等的点.可证△AP
、△AC
、 △PC
均为等边三角形.可求得:①
,所以点M1的坐标为
;…………5分
②,所以点M2的坐标为
;………………………………....6分③点M3与点M2关于x轴对称,所以点M3的坐标为
;………………..…..7分
④点与点A关于y轴对称,所以点
的坐标为
.
综上所述,到直线AP、AC、CP距离相等的点的坐标分别为,
,
,
.…………………………….. 8分
解析:略

练习册系列答案
相关题目
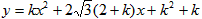 经过坐标原点。
经过坐标原点。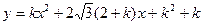 经过坐标原点.
经过坐标原点.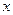 轴的另一个交点,试在
轴的另一个交点,试在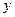 轴上确定一点P,使PA+PB最短,并求出点P的坐标;
轴上确定一点P,使PA+PB最短,并求出点P的坐标;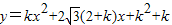 经过坐标原点.
经过坐标原点.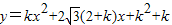 经过坐标原点.
经过坐标原点. 经过坐标原点.
经过坐标原点. 轴的另一个交点,试在
轴的另一个交点,试在 轴上确定一点P,使PA+PB最短,并求出点P的坐标;
轴上确定一点P,使PA+PB最短,并求出点P的坐标;